Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(VT=\left(a+bi\right)^2+\left(a-bi\right)^2\\ =a^2+2abi-b^2+a^2-2abi-b^2\\ =2a^2-2b^2\\ =2\left(a^2-b^2\right)=VP\)
\(VT=\left(a+bi\right)^2-\left(a-bi\right)^2\\ =a^2+2abi-b^2-\left(a^2-2abi-b^2\right)\\ =a^2+2abi-b^2-a^2+2abi+b^2\\ =4abi=VP\)
\(VT=\left(a+bi\right)^2\left(a-bi\right)^2\\ =\left[\left(a+bi\right)\left(a-bi\right)\right]^2\\ =\left[a^2-\left(bi\right)^2\right]^2\\ =\left(a^2+b^2\right)^2=VP\)

\(2\left|z\right|+i\left|z\right|=a+bi-1+2ai-2b+3i\)
\(\Leftrightarrow2\left|z\right|+i\left|z\right|=a-2b-1+\left(2a+b+3\right)i\) \(\Rightarrow\left[{}\begin{matrix}a-2b-1=2\left|z\right|\\2a+b+3=\left|z\right|\end{matrix}\right.\)
\(\Rightarrow3a+4b+7=0\Rightarrow b=\frac{-3a-7}{4}\) thế vào pt đầu
\(a+\frac{3a+7}{2}-1=2\sqrt{a^2+\frac{\left(3a+7\right)^2}{16}}\)
\(\Leftrightarrow5a+5=\sqrt{25a^2+42a+49}\Leftrightarrow\left\{{}\begin{matrix}5a+5\ge0\\\left(5a+5\right)^2=\left(25a^2+42a+49\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a\ge-1\\8a=24\end{matrix}\right.\) \(\Rightarrow a=3\Rightarrow b=-4\Rightarrow S=-1\)

z 2 = ( a + b i ) 2 = a 2 − b 2 + 2abi
( z ) 2 = ( a - b i ) 2 = a 2 − b 2 − 2abi
z.z− = (a + bi)(a − bi) = a 2 + b 2
Từ đó suy ra các kết quả.

\(z+1+2i=\left(1+i\right)\left|z\right|=\left|z\right|+i.\left|z\right|\)
\(\Leftrightarrow z=\left|z\right|-1+\left(\left|z\right|-2\right)i\)
Lấy mođun 2 vế:
\(\Rightarrow\left|z\right|=\sqrt{\left(\left|z\right|-1\right)^2+\left(\left|z\right|-2\right)^2}\)
\(\Leftrightarrow\left|z\right|^2=\left|z\right|^2-2\left|z\right|+1+\left|z\right|^2-4\left|z\right|+4\)
\(\Leftrightarrow\left|z\right|^2-6\left|z\right|+5=0\Rightarrow\left[{}\begin{matrix}\left|z\right|=1\left(l\right)\\\left|z\right|=5\end{matrix}\right.\)
\(\Rightarrow a^2+b^2=5\)
Không đủ dữ kiện để tính \(P=a+b\)

\(\left|z\right|=1\Rightarrow z=cosx+i.sinx\)
\(z^3-z+2=cos3x+i.sin3x-cosx-i.sinx+2\)
\(=\left(cos3x-cosx+2\right)-i.\left(sin3x-sinx\right)\)
\(=\left(2-2sin2x.sinx\right)-i.2cos2x.sinx\)
\(=2\left[\left(1-sin2x.sinx\right)-i.cos2x.sinx\right]\)
\(\Rightarrow A=\left|z^3-z+2\right|=2\sqrt{\left(1-sin2x.sinx\right)^2+cos^22x.sin^2x}\)
\(A=2\sqrt{1-2sin2x.sinx+sin^22x.sin^2x+cos^22x.sin^2x}\)
\(A=2\sqrt{1-4sin^2x.cosx+sin^2x}\)
\(A=2\sqrt{1-4\left(1-cos^2x\right)cosx+1-cos^2x}\)
\(A=2\sqrt{4cos^3x-cos^2x-4cosx+2}\)
\(A_{max}\) khi \(4cos^3x-cos^2x-4cosx+2\) đạt max
Xét hàm \(f\left(t\right)=4t^3-t^2-4t+2\) trên \(\left[-1;1\right]\)
\(f'\left(t\right)=12t^2-2t-4=0\Rightarrow\left[{}\begin{matrix}t=-\frac{1}{2}\\t=\frac{2}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(t\right)\) đạt max tại \(t=-\frac{1}{2}\) hay \(A_{max}\) khi \(a=cosx=-\frac{1}{2}\)
\(\Rightarrow b^2=sin^2x=1-cos^2x=\frac{3}{4}\)
\(\Rightarrow P=2a+4b^2=-1+3=2\)

Chọn C.
Đặt z = a + bi.
Theo giải thiết ta có:
[(a + 1) + (b + 1)i](a - bi - i) + 3i = 9
Suy ra : a( a + 1 + ( b + 1) 2 + a( b + 1) i - ( a + 1) ( b + 1) i = 9 - 3i
Hay a(a + 1) + ( b + 1) 2 - ( b +1) i = 9 -3i
Ta có hệ
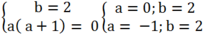
Do ![]() nên a = -1; b = 2 ; a + b = 1.
nên a = -1; b = 2 ; a + b = 1.

\(z\ne4i\Rightarrow\left\{{}\begin{matrix}a\ne0\\b\ne4\end{matrix}\right.\)
\(\frac{z-4}{z-4i}=\frac{a-4+bi}{a+\left(b-4\right)i}=\frac{\left(a-4+bi\right)\left(a-\left(b-4\right)i\right)}{a^2-\left(b-4\right)^2}=\frac{a\left(a-4\right)+b\left(b-4\right)-\left[\left(a-4\right)\left(b-4\right)-ab\right]i}{a^2-\left(b-4\right)^2}\)
Số phức trên là thuần ảo khi và chỉ khi \(\left\{{}\begin{matrix}a\left(a-4\right)+b\left(b-4\right)=0\\\left(a-4\right)\left(b-4\right)-ab\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b-2\right)^2=8\\a+b-4\ne0\end{matrix}\right.\)
\(\Rightarrow\) Tập hợp \(z\) là điểm \(M\left(a;b\right)\) thuộc đường tròn (C) tâm \(I\left(2;2\right)\) bán kính \(R=2\sqrt{2}\) và khác 2 điểm \(A\left(0;4\right)\) và \(B\left(4;0\right)\)
\(P=\left|z\right|^2=a^2+b^2=OM^2\)
\(P_{max}\) khi M trùng giao điểm của đường thẳng OI và đường tròn (giao điểm năm khác phía O so với I)
Phương trình OI: \(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
Giao điểm của OI và (C): \(2\left(x-2\right)^2=8\Rightarrow\left(x-2\right)^2=4\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)
\(\Rightarrow M_1\left(0;0\right)\) (loại); \(M_2\left(4;4\right)\) \(\Rightarrow a=b=4\)
Không có kết quả?!

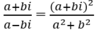
Sử dụng BĐT trị tuyệt đối \(\left\{{}\begin{matrix}\left|x-y\right|\ge\left|x\right|-\left|y\right|\\\left|x-y\right|\ge\left|y\right|-\left|x\right|\end{matrix}\right.\)
\(\Rightarrow-\left|x-y\right|+\left|y\right|\le\left|x\right|\le\left|x-y\right|+\left|y\right|\)
Thay \(x;y\) lần lượt bằng \(z\) và \(a+bi\) với chú ý \(\left|x-y\right|=\left|z-\left(a+bi\right)\right|=c\) rồi chuyển vế là ta được đánh giá nói trên