Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu đặc biệt :
\(\left(3x-2\right)\left(x+1\right)^2\left(3x+8\right)=-16\)
\(\Leftrightarrow9x^4+36x^3+29x^2-14x-16=-16\)
\(\Leftrightarrow9x^4+36x^3+29x^2-14x=0\)
\(\Leftrightarrow x\left(9x^3+36x^2+29x-14\right)=0\)
\(\Leftrightarrow x\left[\left(9x^3+18x^2-7x\right)+\left(18x^2+36x-14\right)\right]=0\)
\(\Leftrightarrow x\left[x\left(9x^2+18x-7\right)+2\left(9x^2+18x-7\right)\right]=0\)
\(\Leftrightarrow x\left(x+2\right)\left(9x^2+18x-7\right)=0\)
\(\Leftrightarrow x\left(x+2\right)\left[\left(9x^2+21x\right)-\left(3x+7\right)\right]=0\)
\(\Leftrightarrow x\left(x+2\right)\left[3x\left(3x+7\right)-\left(3x+7\right)\right]=0\)
\(\Leftrightarrow x\left(x+2\right)\left(3x-1\right)\left(3x+7\right)=0\)
<=> x = 0 hoặc x + 2 = 0 hoặc 3x - 1 = 0 hoặc 3x + 7 = 0
<=> x = 0 hoặc x = - 2 hoặc x = 1/3 hoặc x = 7/3
Vậy phương trình có tập nghiệm là : \(S=\left\{0;\frac{1}{3};\frac{7}{3};-2\right\}\)
Câu 2:
a) Ta có: \(2x^2+3x+1>0\)
\(\Leftrightarrow\frac{2x^2+3x+1}{3}>\frac{0}{3}\)
\(\Leftrightarrow\frac{2}{3}x^2+x+\frac{1}{3}>0\)
=> đpcm
b) Ta có: \(4x-1< 0\)
\(\Leftrightarrow0-\left(4x-1\right)>0\)
\(\Leftrightarrow1-4x>0\)
=> đpcm
c) Ta có: \(\frac{3x-2}{4}+2\frac{1}{2}>0\)
\(\Leftrightarrow\frac{3x-2}{4}+\frac{10}{4}>0\)
\(\Leftrightarrow\frac{3x+8}{4}>0\)
\(\Rightarrow3x+8>0\)
=> đpcm

Mình trình bày lại :
Ta có \(\frac{7x-8}{2x-3}=\frac{4\left(2x-3\right)-\frac{1}{2}\left(2x-3\right)+\frac{5}{2}}{2x-3}=\frac{7}{2}+\frac{5}{2\left(2x-3\right)}\)
Để A đạt giá trị lớn nhất thì 2x-3 đạt giá trị nhỏ nhất. Vì x là số tự nhiên nên 2x-3 là số tự nhiên
=> giá trị nhỏ nhất của 2x-3 là 1 , suy ra x = 2
Vậy Max A = 6 <=> x = 2

Bạn nào trả lời bài này nhanh nhất thì add vs mk , mk sẽ tặng 1 thẻ điện thoại 50k cho 2 bạn trả lời nhanh nhất nhé!
Nhanh các bạn ơi!!!
Hứa k bùng đâu

e sẽ cố gắng !!!
\(3x-15=2x\left(x-5\right)\)
\(3x-15=2x^2-10x\)
\(3x-15-2x^2+10x=0\)
\(13x-15-2x^2=0\)
\(x\left(13-2x\right)-15=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\13-2x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\-2-2x=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\2x=-2\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\x=-1\end{cases}}}\)
\(f,x\left(2x-7\right)-4x+14=0\)
\(2x^2-7x-4x+14=0\)
\(2x^2-11x+14=0\)
\(x\left(2x-11\right)=-14\)
\(\Rightarrow\orbr{\begin{cases}x=-14\\2x-11=-14\end{cases}\Rightarrow\orbr{\begin{cases}x=-14\\2x=-3\end{cases}\Rightarrow}\orbr{\begin{cases}x=-14\\x=-\frac{3}{2}\end{cases}}}\)

a) Đặt: x = a- b; y = b - c ; z = c- a
Ta có: x + y + z = 0
=> \(A=x^3+y^3+z^3=3xyz+\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)=3xyz\)
=> \(A=3xyz=3\left(a-b\right)\left(b-c\right)\left(c-a\right)\)
b) Đặt: \(a=x^2-2x\)
Ta có: \(B=a\left(a-1\right)-6=a^2-a-6=\left(a+2\right)\left(a-3\right)=\left(x^2-2x+2\right)\left(x^2-2x-3\right)\)
\(=\left(x^2-2x+2\right)\left(x+1\right)\left(x-3\right)\)
d) \(D=4\left(x^2+2x-8\right)\left(x^2+7x-8\right)+25x^2\)
Đặt: \(x^2-8=t\)
Ta có: \(D=4\left(t+2x\right)\left(t+7x\right)+25x^2\)
\(=4t^2+36xt+81x^2=\left(2t+9x\right)^2\)
\(=\left(2x^2+9x-16\right)^2\)
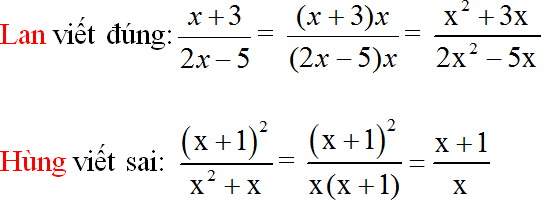
Giải
22003 = 2003 lần chữ số 2 nhân lại.
Vì 2 × 2 × 2 × 2 = 16 (tận cùng là 6)
Mà 6 × 6 × 6 × ... = X (tận cùng là sáu vì 6 × 6 = 36)
Bốn số 2 nhân lại mới được 6 vậy có tổng cộng 2003 số 2 chia 4, tức là thế này:
(2 × 2 × 2 × 2) × (...) × ... = X (có 2003 chữ số 2)
Có tổng cộng 2003 ÷ 4 = 500 (cặp) và dư lại 3 số 2.
Vậy chữ số tận cùng là 6 × ba số hai
=> 6 × 2 × 2 × 2 = 48 (tận cùng là 8)
Vậy bạn Hùng sai !
Ghi chú: thật ra em mới học lớp 5 và biết một tí về toán lớp 6 nên bài này em làm được!
Bạn Hùng giải sai vì :
(29)17 . 2 = 2153 . 2 = 2154 \(\ne\)2155