Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình nghĩ cậu viết sai đề hay j đó rồi
Chắc đề phải như thế này này : \(\sqrt{\left|40\sqrt{2}-57\right|}-\sqrt{40\sqrt{2}+57}\)
Đặt A = \(\sqrt{\left|40\sqrt{2}-57\right|}-\sqrt{40\sqrt{2}+57}\)
A = \(\sqrt{\left|57-40\sqrt{2}\right|}-\sqrt{40\sqrt{2}+57}\)
A = \(\sqrt{57-40\sqrt{2}}-\sqrt{40\sqrt{2}+57}\)
Nhận xét : A < 0 , Bình phương hai vế ta được :
\(A^2=\left(\sqrt{57-40\sqrt{2}}-\sqrt{57+40\sqrt{2}}\right)^2\)
\(A^2=\left(\sqrt{57-40\sqrt{2}}\right)^2+\left(\sqrt{57+40\sqrt{2}}\right)^2-2.\sqrt{\left(57-40\sqrt{2}\right)\left(57+40\sqrt{2}\right)}\)
=> \(A^2=57-40\sqrt{2}+57+40\sqrt{2}-2\sqrt{\left(57-40\sqrt{2}\right)\left(57+40\sqrt{2}\right)}\)
=> \(A^2=114-2\sqrt{57^2-\left(40\sqrt{2}\right)^2}\)
=> \(A^2=114-2\sqrt{3249-3200}\)
\(\Rightarrow A^2=114-2\sqrt{49}\)
\(\Leftrightarrow A^2=114-2.7\)
\(\Leftrightarrow A^2=100\)
=> A = \(\pm\sqrt{100}\) mà A < 0 => A = -10

Lời giải:
Gọi biểu thức cần rút gọn là $P$
Xét tử số: $\sqrt{4+2\sqrt{3}}-\sqrt{3}=\sqrt{3+2\sqrt{3.1}+1}-\sqrt{3}$
$=\sqrt{(\sqrt{3}+1)^2}-\sqrt{3}=|\sqrt{3}+1|-\sqrt{3}=1$
Xét mẫu số:
Ta dự đoán sẽ rút gọn được $\sqrt[3]{17\sqrt{5}-38}$
Đặt $17\sqrt{5}-38=(a+\sqrt{5})^3$ với $a$ nguyên.
$\Leftrightarrow 17\sqrt{5}-38=a^3+15a+\sqrt{5}(3a^2+5)$
$\Rightarrow 17=3a^2+5$ và $-38=a^3+15a$
$\Rightarrow a=-2$
Vậy $17\sqrt{5}-38=(-2+\sqrt{5})^3$
$\Rightarrow (\sqrt{5}+2)\sqrt[3]{17\sqrt{5}-38}=(\sqrt{5}+2)(-2+\sqrt{5})=1$
Vậy $P=\frac{1}{1}=1$

26, đặt bthuc là A suy ra A2=4+4+2\(\sqrt{16-\left(10+2\sqrt{5}\right)}\) suy ra A2=8+2(\(\sqrt{5}\) -1) suy ra A=\(\sqrt{6+2\sqrt{5}}\)=\(\sqrt{5}\)+1
40, tương tự

Bạn xem lại đề. $40\sqrt{2}-57< 0$ nên không thể nằm trong căn được!
Sửa đề: \(\sqrt{57-40\sqrt{2}}-\sqrt{57+40\sqrt{2}}\)
Ta có: \(\sqrt{57-40\sqrt{2}}-\sqrt{57+40\sqrt{2}}\)
\(=\sqrt{32-2\cdot4\sqrt{2}\cdot5+25}-\sqrt{32+2\cdot4\sqrt{2}\cdot5+25}\)
\(=\sqrt{\left(4\sqrt{2}-5\right)^2}-\sqrt{\left(4\sqrt{2}+5\right)^2}\)
\(=4\sqrt{2}-5-4\sqrt{2}-5=-10\)
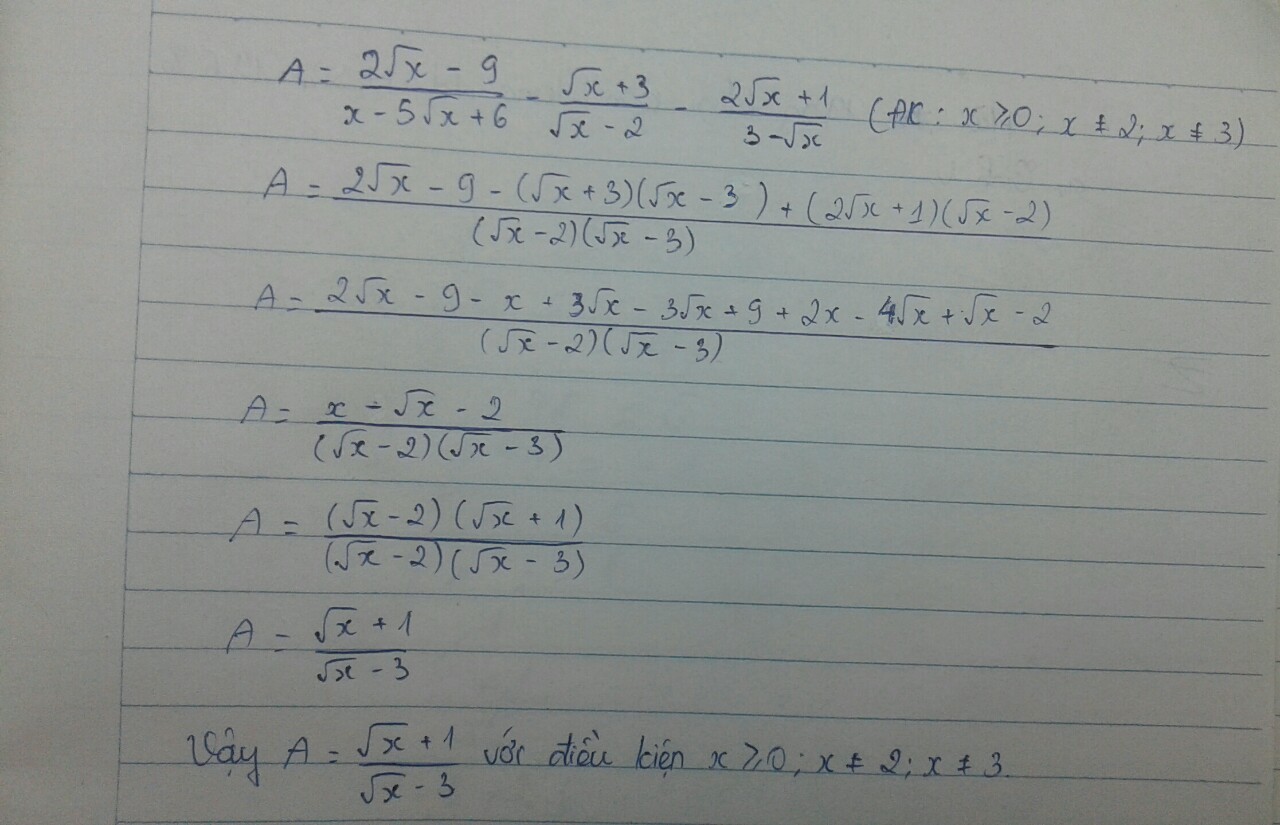 mình trình bày trong hình, hơi mờ bạn thông cảm!
mình trình bày trong hình, hơi mờ bạn thông cảm!