Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}-\frac{3-\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{3+\sqrt{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)
a, \(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt[]{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)

Với `x > 3` có:
`P=[x-3]/\sqrt{x-3}+[x-\sqrt{3x}]/\sqrt{x}`
`P=[(\sqrt{x-3})^2]/\sqrt{x-3}+[\sqrt{x}(\sqrt{x}-\sqrt{3})]/\sqrt{x}`
`P=\sqrt{x-3}+\sqrt{x}-\sqrt{3}`

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
\(P=\left(\dfrac{2}{x-2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}+2}{x-4\sqrt{x}+4}\)
\(=\left(\dfrac{2}{\sqrt{x}\left(\sqrt{x}-2\right)}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)^2}\)
\(=\dfrac{2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}+2}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)

Ta có:\(\frac{a}{b}=\frac{3}{4}\left(1\right)\Rightarrow3b=4a\Rightarrow b=\frac{4a}{3}\left(2\right)\)Theo đề bài nếu cộng 15 đơn vị vào tử thì rút gọn thành \(\frac{7}{9}\)
\(\Rightarrow\frac{a+15}{b}=\frac{7}{9}\)\(\Rightarrow9\left(a+15\right)=7b\Rightarrow9a+135=7b\left(3\right)\)
Từ (1) và (2) suy ra:\(9a+135=7.\left(\frac{4a}{3}\right)\)
\(9a+135-\frac{28a}{3}=0\)
\(\frac{27a}{3}-\frac{28a}{3}+135=0\)
\(135-\frac{a}{3}=0\)
\(\frac{a}{3}=135\Rightarrow a=405\left(4\right)\)
Từ (1) và (4) ta được:\(\frac{405}{b}=\frac{3}{4}\)
\(\Rightarrow b=405.4:3=303,75\)


\(\sqrt{2-\sqrt{3}}=\frac{\sqrt{2}.\sqrt{2-\sqrt{3}}}{\sqrt{2}}=\frac{\sqrt{2.\left(2-\sqrt{3}\right)}}{\sqrt{2}}=\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}=\frac{\sqrt{3-2\sqrt{3}+1}}{\sqrt{2}}=\frac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}=\frac{\left|\sqrt{3}-1\right|}{\sqrt{2}}=\frac{\sqrt{3}-1}{\sqrt{2}}=\frac{\sqrt{2}.\left(\sqrt{3}-1\right)}{\sqrt{2}.\sqrt{2}}=\frac{\sqrt{2}.\sqrt{3}-\sqrt{2}.1}{\sqrt{2.2}}=\frac{\sqrt{2.3}-\sqrt{2}}{\sqrt{4}}=\frac{\sqrt{6}-\sqrt{2}}{2}\)

Câu 2:
a: Ta có: \(P=3x-\sqrt{x^2-10x+25}\)
\(=3x-\left|x-5\right|\)
\(=\left[{}\begin{matrix}3x-x+5=2x+5\left(x\ge5\right)\\3x+x-5=4x-5\left(x< 5\right)\end{matrix}\right.\)
b: Vì x=2<5 nên \(P=4\cdot2-5=8-5=3\)
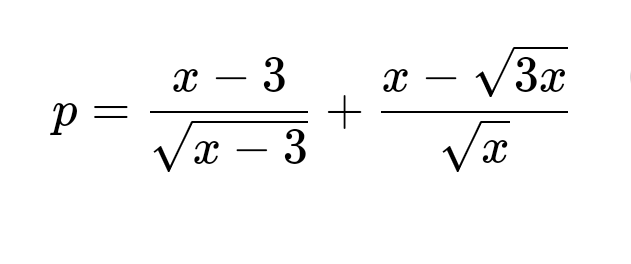
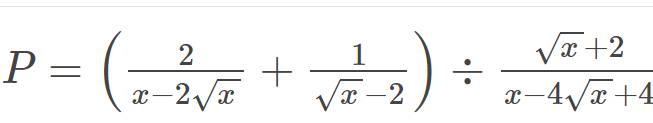 rút gọn P
rút gọn P