Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
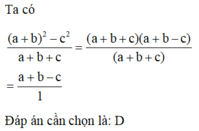
a) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{a+b+c}=a+b-c\)
b ) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{a^2+2ab+b^2-c^2}{a^2+ac+c^2-b^2}\)
\(=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+c+b\right)\left(a+c-b\right)}=\frac{a+b-c}{a-b+c}\)
a) Đặt \(A=\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b\right)^2}{a+b}-\frac{c^2}{c}=a+b-c\)
b)Đặt \(B=\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{a+b-c}{a+c-b}\)
Auto giải thích thêm câu b) (để tránh bị các thành phần spammer bắt bẻ)
\(\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{a+b-c}{a+c-b}\) vì:
\(\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left[\left(a+b\right)-c\right]\left[\left(a+b\right)+c\right]}{\left[\left(a+c\right)-b\right]\left[\left(a+c\right)+b\right]}=\frac{a+b-c}{a+c-b}\)
a ) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{a+b+c}=a+b-c\)
b ) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{a^2+2ab+b^2-c^2}{a^2+2ac+c^2-b^2}\)
\(=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+c+b\right)\left(a+c-b\right)}=\frac{a+b-c}{a-b+c}\)
a) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{a+b+c}=a+b-c\)
b) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{\left(a^2+2ab+b^2\right)-c^2}{\left(a^2+2ac+c^2\right)-b^2}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+c+b\right)\left(a+c-b\right)}=\frac{a+b-c}{a+c-b}\)
a, Gợi ý nà :3
a^2 + b^2 - c^2 +2ab = (a^2 + b^2 + 2ab) -c^2 = (a+b)^2 - c^2 = (a + b - c)(a + b + c)
a^2 - b^2 + c^2 + 2ac = (a + c)^2 - b^2 = (a + b + c)(a - b + c)
b. Gợi ý tiếp luôn nà :3
a^3 + b^3 + c^3 - 3abc
= (a^3 + b^3 +3a^2 x b + 3ab^2) - 3ab(a+b) -3abc + c^3
= (a+b)^3 + c^3 - 3ab(a+b+c)
= (a + b+ c)[(a+b)^2 - c(a+b) +c^2] - 3ab(a+b+c)
=(a+b+c)(a^2 + b^2 + c^2 -ac -bc + 2ab -3ab)
=(a+b+c)(a^2 + b^2 + c^2 - ab - bc -ca)
Rồi cứ thế rút gọn...
Học tốt nha bạn :3
\(\frac{a^2+2ab+b^2-c^2}{a^2+2ac+c^2-b^2}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+b+c\right)\left(a-b+c\right)}=\frac{a+b-c}{a-b+c}\)
\(\text{nhận xét: ta có hằng đẳng thức:}\)
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
đó đến đây bạn làm tiếp
Ta có : \(a+b+c=0\)
\(\Rightarrow a+b=-c\)
\(\Rightarrow a^2+b^2+2ab=c^2\)
\(\Rightarrow c^2-a^2-b^2=2ab\)
Tương tự :
\(b^2-c^2-a^2=2ac\)
\(a^2-b^2-c^2=2ab\)
\(\Leftrightarrow\frac{a^2}{2bc}+\frac{b^2}{2ac}+\frac{c^2}{2ab}=\frac{a^3+b^3+c^3}{2abc}\)
Mà \(a+b+c=0\)\(\Rightarrow a^3+b^3+c^3=3abc\)( cái này rất dễ chứng minh nha , bạn có thể tham khảo trên mạng hoặc nhắn tin cho mình )
\(\Leftrightarrow\frac{a^3+b^3+c^3}{2abc}=\frac{3abc}{2abc}=\frac{3}{2}\)
\(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}\)
\(=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}\)
\(=\frac{\left(a+b-c\right)\left(a+b+c\right)}{\left(a+c-b\right)\left(a+b+c\right)}\)
\(=\frac{a+b-c}{a+c-b}\left(a+b+c\ne0\right)\)
\(\frac{\left(a-b\right)\left(c-d\right)}{\left(b^2-a^2\right)\left(d^2-c^2\right)}=\frac{\left(b-a\right)\left(d-c\right)}{\left(b-a\right)\left(b+a\right)\left(d-c\right)\left(d+c\right)}=\frac{1}{\left(a+b\right)\left(c+d\right)}\)
\(\frac{m^4-m}{2m^2+2m+2}=\frac{m\left(m^3-1\right)}{2m^2+2m+2}=\frac{m\left(m-1\right)\left(m^2+m+1\right)}{2\left(m^2+m+1\right)}=\frac{m\left(m-1\right)}{2}\)
\(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}\)
\(=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}\)
\(=\frac{\left(a+b-c\right)\left(a+b+c\right)}{\left(a+c-b\right)\left(a+c+b\right)}\)
\(=\frac{a+b-c}{a+c-b}\)
Bạn sai đề nên mik sửa và làm luôn nha
