
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

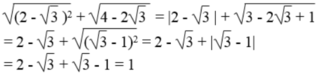


a) \(M=\sqrt{3-2\sqrt{2}}+\sqrt{6+4\sqrt{2}}=\sqrt{2-2\sqrt{2}+1}+\sqrt{2+2.\sqrt{2}.2+4}=\sqrt{\left(\sqrt{2}-1\right)^2}+\sqrt{\left(\sqrt{2}+2\right)^2}=\left|\sqrt{2}-1\right|+\sqrt{2}+2=\sqrt{2}-1+\sqrt{2}+2=2\sqrt{2}+1\)
b) \(N=\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\dfrac{\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}}{\sqrt{2}}=\dfrac{\sqrt{3+2\sqrt{3}+1}+\sqrt{3-2\sqrt{3}+1}}{\sqrt{2}}=\dfrac{\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}=\dfrac{\sqrt{3}+1+\left|\sqrt{3}-1\right|}{\sqrt{2}}=\dfrac{\sqrt{3}+1+\sqrt{3}-1}{\sqrt{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}}=\sqrt{2}.\sqrt{3}=\sqrt{6}\)
Hướng dẫn trả lời:
M=√3−2√2−√6+4√2=√(√2)2−2√2.1+12−√(2)2+2√2+(√2)2=√(√2−1)3−√(2+√2)2=∣∣√2−1∣∣−∣∣2+√2∣∣=√2−1−2−√2=−3M=3−22−6+42=(2)2−22.1+12−(2)2+22+(2)2=(2−1)3−(2+2)2=|2−1|−|2+2|=2−1−2−2=−3
N=√2+√3+√2−√3⇒N2=(√2+√3+√2−√3)2=2+√3+2√(2+√3)(2−√3)+2−√3=4+2√4−3=6N=2+3+2−3⇒N2=(2+3+2−3)2=2+3+2(2+3)(2−3)+2−3=4+24−3=6
Vì N > 0 nên N2 = 6 ⇒ N = √6. Vậy

a) \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=\sqrt{4-3}=\sqrt{1}=1\)
b)
Đặt \(B=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)
\(B^2=4+\sqrt{7}-2\sqrt{\left(4+\sqrt{7}\right)\left(4-\sqrt{7}\right)}+4-\sqrt{7}\)
\(=8-2\sqrt{16-7}=8-2\sqrt{9}=8-2.3=8-6=2\)
\(\Rightarrow B=\sqrt{2}\)

a) \(\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{3}+1-\left(\sqrt{3}-1\right)\)
\(=\sqrt{3}+1-\sqrt{3}+1\)
\(=2\)
b) \(\sqrt{9-4\sqrt{5}}-\sqrt{9+4\sqrt{5}}\)
\(=\sqrt{5}-2-\left(2+\sqrt{5}\right)\)
\(=\sqrt{5}-2-\sqrt{5}-2\)
\(=-4\)
a) \(\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{3+2\sqrt{3}+1}-\sqrt{3-2\sqrt{3}+1}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}+1-\sqrt{3}+1\)
\(=2\)
b) tương tự

a)
\(\sqrt{\left(3-2\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{8}-4\right)^2}=3-2\sqrt{2}-4+\sqrt{8}\)
\(=3-2\sqrt{2}-4+2\sqrt{2}=3-4=-1\)
b)
\(\frac{2}{\sqrt{3}-1}-\frac{2}{\sqrt{3}+1}=\frac{2\left(\sqrt{3}+1\right)-2\left(\sqrt{3}-1\right)}{3-1}\)
\(=\frac{2\left(\sqrt{3}+1-\sqrt{3}+1\right)}{2}=\sqrt{3}+1-\sqrt{3}+1=1+1=2\)

a) \(\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{6}-\sqrt{2}}=\frac{\sqrt{3}-1}{\sqrt{2}\left(\sqrt{3}-1\right)}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)
b) \(\frac{1}{2\sqrt{3}}+\frac{\sqrt{2}}{\sqrt{6}}-\frac{2}{3+\sqrt{3}}=\frac{2\sqrt{3}}{12}+\frac{2\sqrt{3}}{6}-\frac{6-2\sqrt{3}}{6}\)
\(=\frac{2\sqrt{3}}{12}+\frac{4\sqrt{3}}{12}-\frac{12-4\sqrt{3}}{12}=\frac{-12+10\sqrt{3}}{12}=\frac{-6+5\sqrt{3}}{6}\)


a,A.√2= √(4+2√3)-√(4-2√3)
= √(1+√3)2 -√( √3 -1)2
= 1+√3-√3+1= 2
=> A= 2/√2=√2
B2= (4+√15)2.(4-√15).(√10-√6)2
= (4+√15).1.(16-4√15)
= (4+√15).(4-√15).4
= 4
=> B = √4 = 2