Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(x^3-2x^2+3x-6=x\left(x^2+3\right)-2\left(x^2+3\right)=\left(x-2\right)\left(x^2+3\right)\)
b, \(x^2+2x+1-4y^2=\left(x+1\right)^2-\left(2y\right)^2=\left(x+1-2y\right)\left(x+1+2y\right)\)

Bài 1.
a) x( 8x - 2 ) - 8x2 + 12 = 0
<=> 8x2 - 2x - 8x2 + 12 = 0
<=> 12 - 2x = 0
<=> 2x = 12
<=> x = 6
b) x( 4x - 5 ) - ( 2x + 1 )2 = 0
<=> 4x2 - 5x - ( 4x2 + 4x + 1 ) = 0
<=> 4x2 - 5x - 4x2 - 4x - 1 = 0
<=> -9x - 1 = 0
<=> -9x = 1
<=> x = -1/9
c) ( 5 - 2x )( 2x + 7 ) = ( 2x - 5 )( 2x + 5 )
<=> -4x2 - 4x + 35 = 4x2 - 25
<=> -4x2 - 4x + 35 - 4x2 + 25 = 0
<=> -8x2 - 4x + 60 = 0
<=> -8x2 + 20x - 24x + 60 = 0
<=> -4x( 2x - 5 ) - 12( 2x - 5 ) = 0
<=> ( 2x - 5 )( -4x - 12 ) = 0
<=> \(\orbr{\begin{cases}2x-5=0\\-4x-12=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=-3\end{cases}}\)
d) 64x2 - 49 = 0
<=> ( 8x )2 - 72 = 0
<=> ( 8x - 7 )( 8x + 7 ) = 0
<=> \(\orbr{\begin{cases}8x-7=0\\8x+7=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{8}\\x=-\frac{7}{8}\end{cases}}\)
e) ( x2 + 6x + 9 )( x2 + 8x + 7 ) = 0
<=> ( x + 3 )2( x2 + x + 7x + 7 ) = 0
<=> ( x + 3 )2 [ x( x + 1 ) + 7( x + 1 ) ] = 0
<=> ( x + 3 )2( x + 1 )( x + 7 ) = 0
<=> x = -3 hoặc x = -1 hoặc x = -7
g) ( x2 + 1 )( x2 - 8x + 7 ) = 0
Vì x2 + 1 ≥ 1 > 0 với mọi x
=> x2 - 8x + 7 = 0
=> x2 - x - 7x + 7 = 0
=> x( x - 1 ) - 7( x - 1 ) = 0
=> ( x - 1 )( x - 7 ) = 0
=> \(\orbr{\begin{cases}x-1=0\\x-7=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=7\end{cases}}\)
Bài 2.
a) ( x - 1 )2 - ( x - 2 )( x + 2 )
= x2 - 2x + 1 - ( x2 - 4 )
= x2 - 2x + 1 - x2 + 4
= -2x + 5
b) ( 3x + 5 )2 + ( 26x + 10 )( 2 - 3x ) + ( 2 - 3x )2
= 9x2 + 30x + 25 - 78x2 + 22x + 20 + 9x2 - 12x + 4
= ( 9x2 - 78x2 + 9x2 ) + ( 30x + 22x - 12x ) + ( 25 + 20 + 4 )
= -60x2 + 40x2 + 49
d) ( x + y )2 - ( x + y - 2 )2
= [ x + y - ( x + y - 2 ) ][ x + y + ( x + y - 2 ) ]
= ( x + y - x - y + 2 )( x + y + x + y - 2 )
= 2( 2x + 2y - 2 )
= 4x + 4y - 4
Bài 3.
A = 3x2 + 18x + 33
= 3( x2 + 6x + 9 ) + 6
= 3( x + 3 )2 + 6 ≥ 6 ∀ x
Đẳng thức xảy ra <=> x + 3 = 0 => x = -3
=> MinA = 6 <=> x = -3
B = x2 - 6x + 10 + y2
= ( x2 - 6x + 9 ) + y2 + 1
= ( x - 3 )2 + y2 + 1 ≥ 1 ∀ x,y
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-3=0\\y^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=0\end{cases}}\)
=> MinB = 1 <=> x = 3 ; y = 0
C = ( 2x - 1 )2 + ( x + 2 )2
= 4x2 - 4x + 1 + x2 + 4x + 4
= 5x2 + 5 ≥ 5 ∀ x
Đẳng thức xảy ra <=> 5x2 = 0 => x = 0
=> MinC = 5 <=> x = 0
D = -2/7x2 - 8x + 7 ( sửa thành tìm Max )
Để D đạt GTLN => 7x2 - 8x + 7 đạt GTNN
7x2 - 8x + 7
= 7( x2 - 8/7x + 16/49 ) + 33/7
= 7( x - 4/7 )2 + 33/7 ≥ 33/7 ∀ x
Đẳng thức xảy ra <=> x - 4/7 = 0 => x = 4/7
=> MaxC = \(\frac{-2}{\frac{33}{7}}=-\frac{14}{33}\)<=> x = 4/7

\(3x\left(x-5\right)-x\left(4+3x\right)=43\)
\(\Leftrightarrow3x^2-15x-4x-3x^2=43\)
\(\Leftrightarrow-19x=43\)
\(\Leftrightarrow x=\frac{-43}{19}\)

1) (3x+4)(x+1) = 3x2+7x+4 đặt là a
(6x+7)2= 36x2+84x+49 = 12a+1
=> a(12a+1)- 6 = 12a2 -a -6 = (3a+2)(4a-3) = (9x2+21x+14)(12x2+28x+13)
2) (x-2)2=x2-4x+4 đặt là a
(2x-5)(2x-3)= 4x2-16x+15 =4a-1
=> a(4a-1)-5 = 4a2-a-5 = (4a-5)(a+1) = ( 4x2-16x+11)(x2-4x+5)
3) đặt (x+3)2 =a ta làm tương tự
4) (x-2)(x-10)(x-4)(x-5) = (x2-12x+20)(x2-9x+20)
đặt x2+20=a => (a-12x)(a-9x)-54x2 = a2-21ax+54x2 = (a-18x)(a-3x) = (x2-18x+20)(x2-3x+20)

1) \(2x.\left(x-7\right)-\left(x+3\right)\left(x-2\right)-\left(x+4\right)\left(x-4\right)\)
\(=2x^2-14x-\left(x^2+x-6\right)-\left(x^2-4\right)\)
\(=-15x+10\)
b) \(2x.\left(x+1\right)^2-\left(x-1\right)^3-\left(x-2\right)\left(x^2+2x+4\right)\)
\(=2x.\left(x^2+2x+1\right)-\left(x^3-3x^2+3x-1\right)-\left(x^3-8\right)\)
\(=2x^3+4x^2+2x-x^3+3x^2-3x+1-x^3+8\)
\(=7x^2-x+9\)
c) \(\left(x-5\right)\left(x+5\right)\left(x+2\right)-\left(x+2\right)^3\)
\(=\left(x+2\right).\left[\left(x-5\right)\left(x+5\right)-\left(x+2\right)^2\right]\)
\(=\left(x+2\right).\left(x^2-25-x^2-4x-4\right)\)
\(=\left(x+2\right)\left(-4x-29\right)\)
\(=-4x^2-37x-58\)
d) \(\left(x-3\right)^3+\left(x-5\right)\left(x^2+5x+25\right)-\left(x-1\right)\left(x^2+x+1\right)\)
\(=x^3-9x^2+27x-27+\left(x^3-125\right)-\left(x^3-1\right)\)
\(=x^3-9x^2+27x-151\)
e) \(\left(x-1\right)^3-\left(x-2\right)\left(x^2-2x+4\right)+3x^2+2x\)
\(=x^3-3x^2+3x-1-\left(x^3-8\right)+3x^2+2x\)
\(=5x+7\)
Nhẩm ấy, ko nháp âu
\(2x\left(x-7\right)-\left(x+3\right)\left(x-2\right)-\left(x+4\right)\left(x-4\right)\)
\(=2x^2-14x-\left(x^2-2x+3x-6\right)-\left(x^2-4x+4x-16\right)\)
\(=2x^2-14x-x^2+x-6-x^2+16\)
\(=-13x-10\)
\(2x\left(x+1\right)^2-\left(x-1\right)^3-\left(x-2\right)\left(x^2+2x+4\right)\)
\(=2x\left(x^2+2x+1\right)-\left(x^3-3x^2+3x-1\right)-\left(x-2\right)\left(x+2\right)\)
\(-2x^3+4x^2+2x-x^3+3x^2-3x+1-x^2+4\)
\(=-3x^3+6x^2-x+5\)

1.a) 2x4-4x3+2x2
=2x2(x2-2x+1)
=2x2(x-1)2
b) 2x2-2xy+5x-5y
=2x(x-y)+5(x-y)
=(2x+5)(x-y)
2.
a) 4x(x-3)-x+3=0
=>4x(x-3)-(x-3)=0
=>(4x-1)(x-3)=0
=> 2 TH:
*4x-1=0 *x-3=0
=>4x=0+1 =>x=0+3
=>4x=1 =>x=3
=>x=1/4
vậy x=1/4 hoặc x=3
b) (2x-3)^2-(x+1)^2=0
=> (2x-3-x-1).(2x-3+x+1)=0
=>(x-4).(3x-2)=0
=> 2 TH
*x-4=0
=> x=0+4
=> x=4
*3x-2=0
=>3x=0-2
=>3x=-2
=>x=-2/3
vậy x=4 hoặc x=-2/3

1) \(x^3+x^2+4\)
\(=\left(x^3-x^2+2x\right)+\left(2x^2-2x+4\right)\)
\(=x\left(x^2-x+2\right)+2\left(x^2-x+2\right)\)
\(=\left(x^2-x+2\right)\left(x+2\right)\)
2) \(x^3-2x-4\)
\(=\left(x^3+2x^2+2x\right)-\left(2x^2+4x+4\right)\)
\(=x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\)
\(=\left(x^2+2x+2\right)\left(x-2\right)\)

a) ( x - 1 )( 2x + 1 ) + 3( x - 1 )( x + 2 )( 2x + 1 )
= ( x - 1 )( 2x + 1 )[ 1 + 3( x + 2 ) ]
= ( x - 1 )( 2x + 1 )( 1 + 3x + 6 )
= ( x - 1 )( 2x + 1 )( 3x + 7 )
b) ( 6x + 3 ) - ( 2x - 5 )( 2x + 1 )
= 3( 2x + 1 ) - ( 2x - 5 )( 2x + 1 )
= ( 2x + 1 )[ 3 - ( 2x - 5 ) ]
= ( 2x + 1 )( 3 - 2x + 5 )
= ( 2x + 1 )( 8 - 2x )
= 2( 2x + 1 )( 4 - x )
c) ( x - 5 )2 + ( x + 5 )( x - 5 ) - ( 5 - x )( 2x + 1 )
= ( x - 5 )2 + ( x + 5 )( x - 5 ) + ( x - 5 )( 2x + 1 )
= ( x - 5 )[ ( x - 5 ) + ( x + 5 ) + ( 2x + 1 ) ]
= ( x - 5 )( x - 5 + x + 5 + 2x + 1 )
= ( x - 5 )( 4x + 1 )
d) ( 3x - 2 )( 4x - 3 ) - ( 2 - 3x )( x - 1 ) - 2( 3x - 2 )( x + 1 )
= ( 3x - 2 )( 4x - 3 ) + ( 3x - 2 )( x - 1 ) - 2( 3x - 2 )( x + 1 )
= ( 3x - 2 )[ ( 4x - 3 ) + ( x - 1 ) - 2( x + 1 ) ]
= ( 3x - 2 )( 4x - 3 + x - 1 - 2x - 2 )
= ( 3x - 2 )( 3x - 6 )
= 3( 3x - 2 )( x - 2 )
jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjj

Bài 1:
a) (3x-2).(4x+5)-6x.(2x-1) = 12x^2 +15x - 8x -10 - 12x^2 + 6x = 13x - 10
b) (2x-5)^2 - 4.(x+3).(x-3) = 4x^2 - 20x + 25 - 4x^2 + 12x -12x + 36 = -20x + 61
Bài 2:
a)(2x-1)^2-(x+3)^2 = 0
<=> (2x-1-x-3).(2x-1+x+3) =0
<=>(x-4).(3x+2) = 0
<=> x-4 = 0 hoặc 3x+2=0
*x-4=0 => x=4
*3x+2 = 0 => 3x=-2 => x=-2/3
b)x^2(x-3)+12-4x=0 <=> x^2(x-3) - 4(x-3) =0 <=> (x-3).(x-2)(x+2) <=> x-3=0 hoặc x-2=0 hoặc x+2 =0
*x-3=0 => x=3
*x-2=0 =>x=2
*x+2=0 =>x=-2
c) 6x^3 -24x =0 <=> 6x(x^2 -4)=0 <=> 6x(x-2)(x+2)=0 <=> x=0 hoặc x-2 =0 hoặc x+2=0 <=> x=0 hoặc x=2 hoặc x=-2
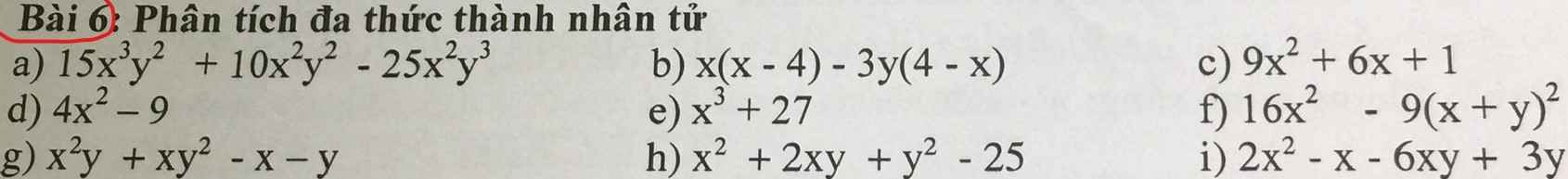
1: \(\left(2x+3\right)^2-2\left(2x+3\right)\left(2x+5\right)+\left(2x+5\right)^2\)
\(=\left(2x+3-2x-5\right)^2\)
=4