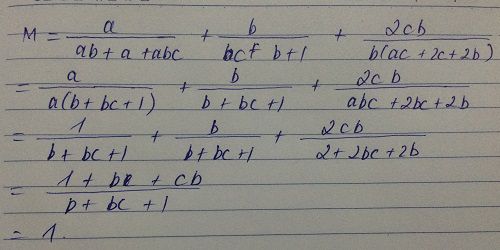Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


thế abc=2 vào M ta có
M=\(\frac{a}{ab+b+abc}\)+ \(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac+abc^2+abc}\)
M=\(\frac{a}{a\left(bc+b+1\right)}\)+\(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac\left(bc+b+1\right)}\)
M=\(\frac{bc+b+1}{bc+b+1}\)=1
1 nha bạn cho mình nha

\(\frac{a}{ab+a+2}\)+ \(\frac{b}{bc+b+1}\)+ \(\frac{2c}{ac+2c+2}\)
= \(\frac{a}{ab+a+2}\)+ \(\frac{ab}{a\left(bc+b+1\right)}\)+ \(\frac{2abc}{ab\left(ac+2c+2\right)}\)
= \(\frac{a}{ab+a+2}\)+ \(\frac{ab}{abc+ab+a}\)+ \(\frac{2abc}{a^2bc+2abc+2ab}\)
= \(\frac{a}{ab+a+2}\)+ \(\frac{ab}{ab+a+2}\)+ \(\frac{2}{ab+a+2}\) (vì abc = 2 )
= \(\frac{ab+a+2}{ab+a+2}\)= 1

M\(=\dfrac{a}{ab+a+2}+\dfrac{b}{bc+b+1}+\dfrac{2c}{ac+2c+2}\)
\(M=\dfrac{a}{ab+a+abc}+\dfrac{b}{bc+b+1}+\dfrac{2bc}{b\left(ac+2c+2\right)}\)
M = \(\dfrac{a}{a\left(b+1+bc\right)}+\dfrac{b}{b+1+bc}+\dfrac{2bc}{abc+2bc+2b}\)
M=\(\dfrac{1}{b+1+bc}+\dfrac{b}{b+1+bc}+\dfrac{2bc}{2+2bc+2b}\)
M = \(\dfrac{1+b}{b+1+bc}+\dfrac{2bc}{2\left(1+bc+b\right)}\)
M = \(\dfrac{1+b}{b+1+bc}+\dfrac{bc}{b+1+bc}=\dfrac{1+b+bc}{b+1+bc}=1\)

Vì \(abc=2\)nên ta có:
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(1+bc+b\right)}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+c+1}\)
\(=\frac{1+b+bc}{bc+c+1}=1\)

Ta có ; \(\frac{a}{ab+a+2}\)+\(\frac{b}{bc+b+1}\)+\(\frac{c}{ac+2c+2}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{abc+ab+a}\)+\(\frac{c}{ac+2c+abc}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{c}{c\left(a+2+ab\right)}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{1}{a+ab+2}\)
=\(\frac{a+ab+1}{ab+a+2}\)
Đề bài này hình như có gì sai bạn ạ
đáng ra phải là \(\frac{2c}{ac+2c+2}\) chứ
À xin lỗi nha mình nhập sai. đúng là : \(\frac{2c}{ac+2c+2}\)

\(M=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{abc+2bc+2b}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2bc}{2+2bc+2b}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1+b+bc}{b+1+bc}=1\)
Vậy \(M=1.\)

Thay abc = 2 vào biểu thức A ta được:
\(A=\dfrac{a}{ab+a+abc}+\dfrac{b}{bc+b+1}+\dfrac{abc\cdot c}{ac+abc+abc}\\ A=\dfrac{1}{b+1+bc}+\dfrac{b}{bc+b+1}+\dfrac{bc}{1+bc+b}\\ A=\dfrac{1+b+bc}{1+b+bc}\\ A=1\)
Hàng thứ 2 phải sửa lại như vậy:
\(A=\dfrac{a}{ab+a+abc}+\dfrac{b}{bc+b+1}+\dfrac{abc.c}{ac+abc.c+abc}\)