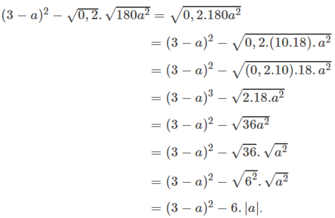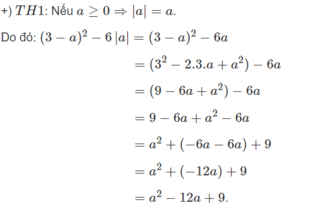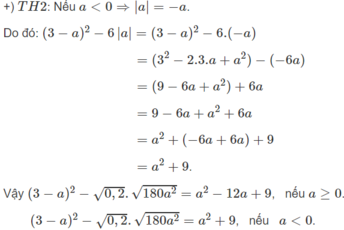Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
3√5a - √20a + 4√45a + √a = 3√5a - 2√5a + 4.3√5a + √a
= 3√5a - 2√5a + 12√5a + √a = 13√5a + √a
3√5a - √20a + 4√45a + √a = 3√5a - 2√5a + 4.3√5a + √a
= 3√5a - 2√5a + 12√5a + √a = 13√5a + √a
\(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\)\(a\ge0\)
\(\Leftrightarrow3\sqrt{5a}-2\sqrt{5a}+12\sqrt{5a}+\sqrt{a}\)
\(\Leftrightarrow13\sqrt{5a}+\sqrt{a}\)
VẬY BIỂU THỨC ĐÃ CHO \(=13\sqrt{5a}+\sqrt{a}\)
Cách hỏi của bạn thực sự hơi khó hiểu. Mình chỉ trả lời theo cách hiểu của mình về câu hỏi của bạn thôi nhé.
- Thứ nhất, không cần phải tìm điều kiện của số trong giá trị tuyệt đối. Thông thường khi đến đoạn $\sqrt{a^2}=|a|$ thì đề bài đã có sẵn điều kiện $a\geq 0$ hoặc $a< 0$ để bạn tiếp tục thực hiện đến đoạn phá trị tuyệt đối. Ví dụ, cho $a< 0$ thì $\sqrt{a^2}=|a|=-a$
- Thứ hai, trong trường hợp $\sqrt{5a}.\sqrt{45a}-3a$, điều kiện để biểu thức này có nghĩa là $5a\geq 0$ và $45a\geq 0$, hay $a\geq 0$.
Khi đó, để phá căn và xuất hiện trị tuyệt đối, bạn thực hiện $\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\sqrt{(15a)^2}-3a=|15a|-3a=15a-3a=12a$
Do a ≥ 0 nên bài toán luôn xác định. Ta có:
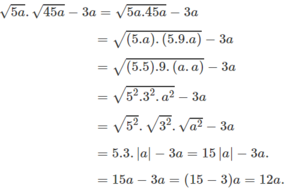
(Vì a ≥ 0 nên |a| = a)
a) Ta có:
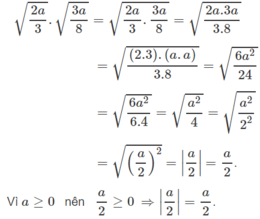
b) Ta có:
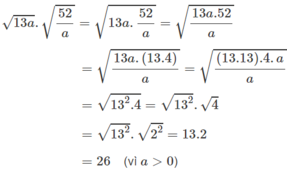
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:
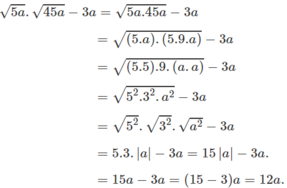
(Vì a ≥ 0 nên |a| = a)
d) Ta có:
