Question

[Thu Trang]

Rút gọn biểu thức:

a) \(\sqrt{6x^2-6x\sqrt{6}+9}\) tại x = \(\sqrt{\dfrac{3}{2}}-\sqrt{\dfrac{2}{3}}\)

b) \(\sqrt{9\times\left(1-6x+9x^2\right)}\) tại x = \(-\sqrt{2}\)

c) \(\sqrt{1-6a+9a^2}+3a\) tại a = \(\dfrac{2}{3}\)

Giải gấp mình trong ngày hôm nay luôn nha, mình cần gấp lắm!!! :((

Answer 1

[Nhiên An Trần]

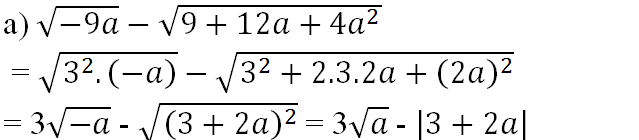
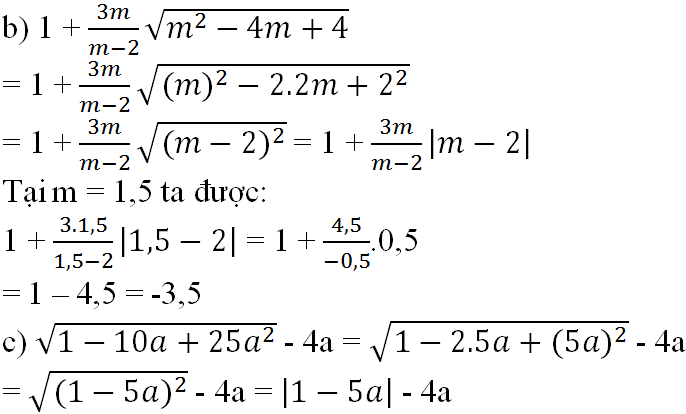
a, \(\sqrt{6x^2-6x\sqrt{6}+9}\)

\(=\sqrt{\left(x\sqrt{6}+3\right)^2}\)

\(=x\sqrt{6}+3\)

Thay \(x=\sqrt{\dfrac{3}{2}}-\sqrt{\dfrac{2}{3}}\)vào biểu thức ta có:

\(\sqrt{6}\left(\sqrt{\dfrac{3}{2}}-\sqrt{\dfrac{2}{3}}\right)+3\)

\(=\sqrt{9}-\sqrt{4}+3\)

\(=3-2+3=4\)

b, \(\sqrt{9\left(1-6x+9x^2\right)}\)

\(=\sqrt{9\left(1-3x\right)^2}\)

\(=3\left(1-3x\right)\)

Thay \(x=-\sqrt{2}\) vào biểu thức ta có:

\(3\left(1-3.\left(-\sqrt{2}\right)\right)\)

\(=3\left(1+3\sqrt{2}\right)\)

\(=3+9\sqrt{2}\)

c, \(\sqrt{1-6a+9a^2}+3a\)

\(=\sqrt{\left(1-3a\right)^2}+3a\)

\(=1-3a+3a=1\)

Nó bằng 1 rồi nên khỏi thay nhé

Answer 2

[Thu Trang]

cảm ơn bạn nhiều nhé!