Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a,\left(2a-3\right)\left(a+1\right)+\left(a^2+6a+9\right):\left(a+3\right)\\ =2a^2-a-3+\left(a+3\right)^2:\left(a+3\right)\\ =2a^2-a-3+a+3\\ =2a^2\\ b,\left(3x-5y\right)\left(-xy\right)^2-3x^2y^2+4x^2y^3\\ =3x^3y^2-5x^2y^3-3x^2y^2+4x^2y^3\\ =3x^3y^2-3x^2y^2-x^2y^3\\ c,x\left(x-2\right)^2-\left(x+2\right)\left(x^2-2x+4\right)+4x^2\\ =x^3-4x^2+4x-x^3-8+4x^2\\ =4x-8\)

\(A=\left(a+b+c\right)^3+\left(a-b-c\right)^3-6a\left(b+c\right)^2\)
\(=\left[a+\left(b+c\right)\right]^3+\left[a-\left(b+c\right)\right]^3-6a\left(b+c\right)^2\)
\(=a^3+3a^2\left(b+c\right)+3a\left(b+c\right)^2+\left(b+c\right)^3+a^3-3a^2\left(b+c\right)+3a\left(b+c\right)^2-\left(b+c\right)^3-6a\left(b+c\right)^2\)
\(=2a^3\)

a) a ≠ 0 , a ≠ − 5
b) Ta có A = a 3 + 4 a 2 − 5 a 2 a ( a + 5 ) = a ( a − 1 ) ( a + 5 ) 2 a ( a + 5 ) = a − 1 2
c) Thay a = -1 (TMĐK) vào a ta được A = -1
d) Ta có A = 0 Û a = 1 (TMĐK)

\(B=\dfrac{\left(a+3\right)^2}{2a^2+6a}\cdot\dfrac{1-6a-18}{a^2-9}\\ a,ĐK:a\ne0;a\ne\pm3\\ b,B=\dfrac{\left(a+3\right)^2}{2a\left(a+3\right)}\cdot\dfrac{-17-6a}{\left(a-3\right)\left(a+3\right)}=\dfrac{-17-6a}{2a\left(a-3\right)}\\ c,B=0\Leftrightarrow-17-6a=0\Leftrightarrow a=-\dfrac{17}{6}\left(tm\right)\\ d,B=1\Leftrightarrow-17-6a=2a^2-6a\\ \Leftrightarrow2a^2=-17\Leftrightarrow a\in\varnothing\)
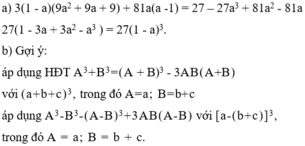
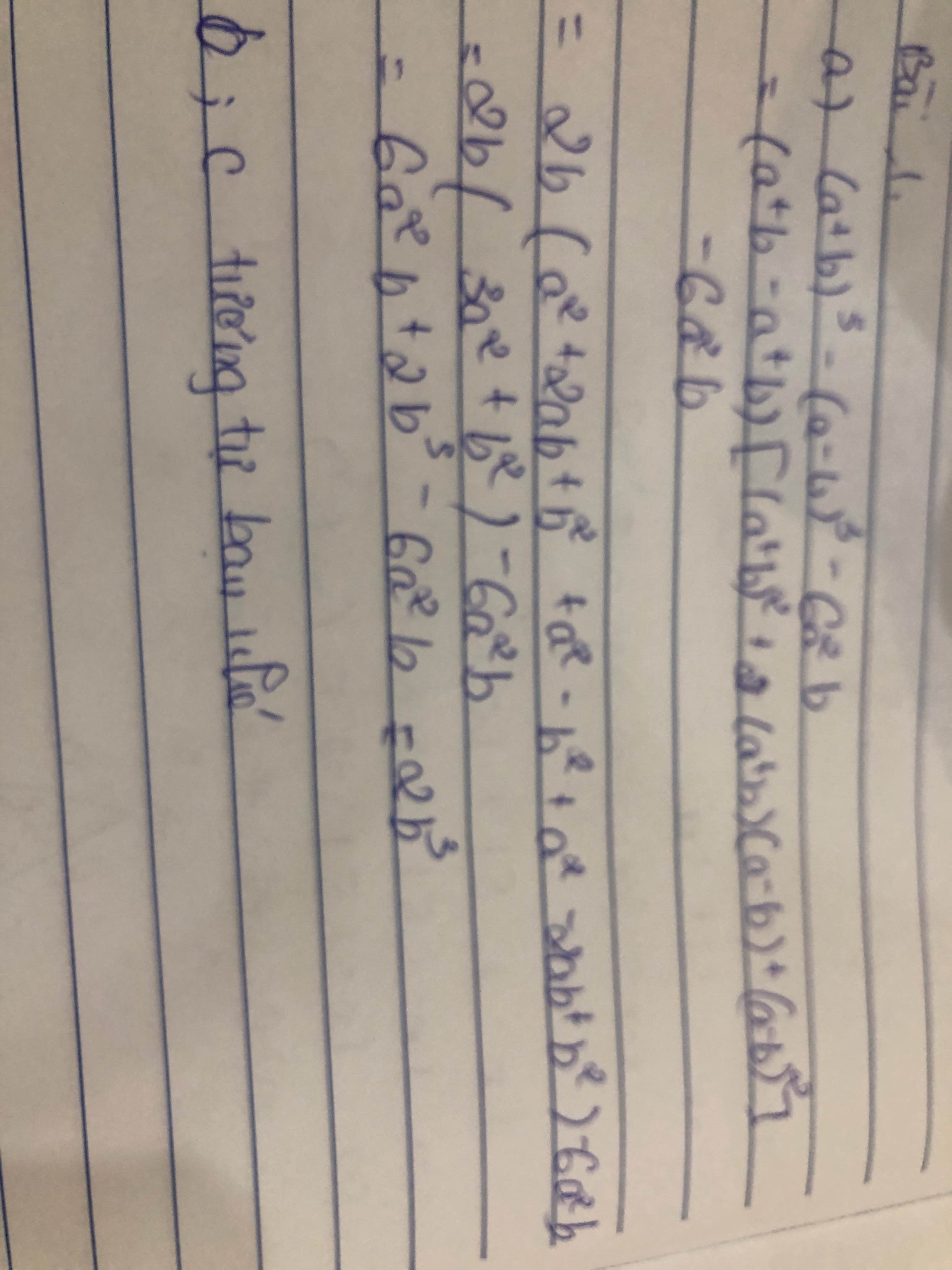
Lời giải:
a.
$(5a+5)^2+10(a-3)(1+a)+a^2-6a+9$
$=(5a+5)^2+2(a-3)(5a+5)+(a-3)^2$
$=(5a+5+a-3)^2$
$=(6a+2)^2$
b.
$B=(a-b)^3-3(b-a)^2c+3(a-b)c^2-c^3$
$=(a-b)^3-3(a-b)^2c+3(a-b)c^2-c^3$
$=(a-b-c)^3$