Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
Vì tanα = 3/5 nên cosα ≠ 0, chia tử và mẫu của biểu thức cho cosα, ta được:
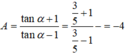

Vì tanα = 2cotα và 3π/2 < α < 2π nên 3π/2 < α < 7π/4.
Do đó sinα < (- 2 )/2 và cosα < 2 /2.
Vì vậy sinα + cosα < 0.
Suy ra các phương án A, C, D bị loại.
Đáp án: B

Ta có sinα + cosα > 0 và sinαcosα > 0. Do đó
( sin α + cos α ) 2 = sin 2 α + cos 2 α + 2 sin α cos α
= 1 + 2sinαcosα > 1
Từ đó suy ra: sinα + cosα > 1

Vì π < α < 5π/4 nên 2π < 2α < 5π/2. Suy ra cot2α > 0. Do đó các phương án A, B, C đều bị loại.
Đáp án: D

+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
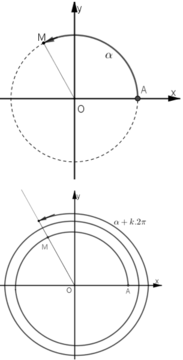
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
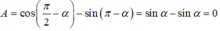
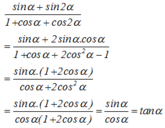


 .
.
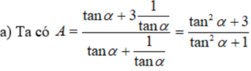
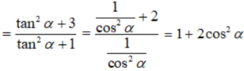

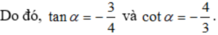
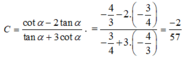
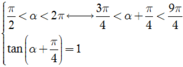
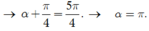

\(A=\frac{4sin2a}{1-2cos^2\frac{a}{2}}=\frac{4\left(2sina.cosa\right)}{1-\left(1+cosa\right)}=\frac{8sina.cosa}{-cosa}=-8sina\)
\(B=\frac{1+cosa-sina}{1-cosa-sina}=\frac{1+2cos^2\frac{a}{2}-1-2sin\frac{a}{2}cos\frac{a}{2}}{1-\left(1-2sin^2\frac{a}{2}\right)-2sin\frac{a}{2}cos\frac{a}{2}}=\frac{2cos^2\frac{a}{2}-2sin\frac{a}{2}cos\frac{a}{2}}{2sin^2\frac{a}{2}-2sin\frac{a}{2}cos\frac{a}{2}}\)
\(=\frac{-cos\frac{a}{2}\left(2sin\frac{a}{2}-2cos\frac{a}{2}\right)}{sin\frac{a}{2}\left(2sin\frac{a}{2}-2cos\frac{a}{2}\right)}=\frac{-cos\frac{a}{2}}{sin\frac{a}{2}}=-cot\frac{a}{2}\)