K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 9 2019
a , Do cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế ở hai đầu dây nên ta có :
\(\frac{I_1}{I_2}=\frac{U_1}{U_2}\Leftrightarrow\)\(\frac{0,4}{I_2}=\frac{6}{30}=\frac{1}{5}\Leftrightarrow I_2=\frac{0,4.5}{1}=2A\)
b , Tóm tắt : \(U_1\)= 6 V
\(U_2\)= ? ; \(I_1\)= 0,4 A ; \(I_2\)= 0,75 A
Tương tự câu a , ta có :
\(\frac{I_1}{I_2}=\frac{U_1}{U_2}\Leftrightarrow\)\(U_2=\frac{6.0,75}{0,4}=11,25V\)
3 tháng 6 2021
(cái đầu tiên mũ 2 thôi nhỉ? chứ mũ 22 sao làm được)
\(A=4m^2+32m+124\\ A=\left(2m\right)^2+2.2m.8+8^2+60\\ A=\left(2m+8\right)^2+60\ge60\forall x\)
\("="\Leftrightarrow\left(2m+8\right)^2=0\\ \Leftrightarrow m=4\)
\(A_{min}=60\)
8 tháng 11 2021
Bài 1:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+5\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
8 tháng 11 2021
Bài 1:
\(b,\) PTHDGD là \(x+2=-2x+5\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow A\left(1;3\right)\)
Vậy A(1;3) là giao điểm 2 đths
\(c,\) PT giao Ox là \(y=0\Leftrightarrow x=-2\Leftrightarrow B\left(-2;0\right)\Leftrightarrow OB=\left|-2\right|=2\)
PT giao Oy là \(x=0\Leftrightarrow y=-2\Leftrightarrow C\left(0;-2\right)\Leftrightarrow OC=\left|-2\right|=2\)
Do đó \(\tan\widehat{OBC}=\dfrac{OC}{OB}=1\Leftrightarrow\widehat{OBC}=45^0\)
Mà hệ số a của đt >0 nên góc tạo bởi đt với Ox là góc nhọn có sđ 45o
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1
Đầu tiên ta luôn luôn đưa hệ số của bình phương về 1 bằng cách đặt nhân tử chung:
\(2m^2-3m+1=2\left(m^2-\dfrac{3}{2}m+\dfrac{1}{2}\right)\)
Sau đó là tận dụng hằng đẳng thức: \(\left(a-b\right)^2=a^2-2ab...\) , ở đây vai trò của a là m và vai trò của 2ab là \(-\dfrac{3}{2}m\)
Nghĩa là ta phải tách \(\dfrac{3}{2}m\) về dạng 2ab với a là m, hay nó là: \(2.m.b\)
\(\Rightarrow-\dfrac{3}{2}m=2mb\)
\(\Rightarrow b=\left(\dfrac{3}{2}m\right):\left(2m\right)=\dfrac{3}{4}\)
\(\Rightarrow b^2=\dfrac{9}{16}\)
Vậy ta cần thêm bớt 9/16 vào
\(2\left(m^2-\dfrac{3}{2}m+\dfrac{1}{2}\right)=2\left(m^2-\dfrac{3}{2}m+\dfrac{9}{16}-\dfrac{9}{16}+\dfrac{1}{2}\right)\)
\(=2\left(m^2-2.m.\dfrac{3}{2}+\dfrac{9}{16}-\dfrac{1}{16}\right)=2\left[\left(m-\dfrac{3}{2}\right)^2-\dfrac{1}{16}\right]\)
\(=2\left(m-\dfrac{3}{2}\right)^2-\dfrac{1}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1
Cách sử dụng máy tính cầm tay:
Ví dụ cần tách đa thức bậc 2 dạng \(ax^2+bx+c\)
Đa thức này luôn tách được về dạng:
\(a\left(x-X_{max-min}\right)^2+Y_{max-min}\) (1)
Cách làm:
Nhập giải pt bậc 2 (tùy dòng máy, ví dụ FX 570 là Mode 5-3)
Nhập các hệ số, sau đó nhấn = liên tục, đến khi thấy nó hiện:
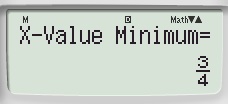
Vậy \(X_{min}=\dfrac{3}{4}\) (nếu hệ số a âm sẽ ra Xmax, hệ số a dương ra Xmin)
Bấm tiếp dấu =, nó ra:
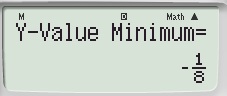
Vậy \(Y_{min}=-\dfrac{1}{8}\)
Thay vào (1) ta được:
\(2m^2-3m+1=2\left(m-\dfrac{3}{4}\right)^2-\dfrac{1}{8}\)
Mất 3s mà ko cần nghĩ cách tách mệt đầu :D
26 tháng 9 2021
c: Ta có: \(\sqrt{x+4\sqrt{x-4}}=5\)
\(\Leftrightarrow\sqrt{x-4}+2=5\)
\(\Leftrightarrow\sqrt{x-4}=3\)
\(\Leftrightarrow x-4=9\)
hay x=13
26 tháng 9 2021
c: Ta có: √x+4√x−4=5x+4x−4=5
⇔√x−4+2=5⇔x−4+2=5
⇔√x−4=3⇔x−4=3
⇔x−4=9⇔x−4=9
hay x=13
23 tháng 3 2016
những lời đồn đại không có ý nghĩa gì hết nêú bạn tin vào cô ấy.và chính tôi cũng rất muốn nghe bạn có tin tưởng vào cô ấy hay không?nếu có thì hãy cứ coi những lời nói đồn đại ấy là ngọn gió thổi qua tai bạn nhé
PA
1
27 tháng 6 2021
Với \(n\in N;n>0\) có:
\(\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\dfrac{1}{\sqrt{n\left(n+1\right)}\left(\sqrt{n+1}+\sqrt{n}\right)}=\dfrac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n\left(n+1\right)}\left(n+1-n\right)}=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)
Áp dụng vào P có:
\(P=1-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{2016}}-\dfrac{1}{\sqrt{2017}}\)
\(=1-\dfrac{1}{\sqrt{2017}}\)
\(\Rightarrow a^2+b=1^2+2017=2018\)
Ý A
KH
4 tháng 7 2021
Dạng tổng quát: \(ax^2+bx+c\) hoặc \(ax+b\sqrt{x}+c\)
Khi đó em tìm: \(a.c=?\)
Ví dụ: \(-3x+10\sqrt{x}-7\) có \(a.c=\left(-3\right).\left(-7\right)=21\)
Sau đó em phân tích số đấy ra thành tích 2 số: \(21=\left(-3\right).\left(-7\right)=3.7\)
Và tổng của 2 số nào bằng \(b\) thì em tách \(bx\) thành 2 số đó (nhớ kèm ẩn x)
\(21=3.7\) và \(b=3+7=10\) nên ta tách thành: \(-3x+3\sqrt{x}+7\sqrt{x}-7\)
Lúc này đặt nhân tử chung thôi!
\(-3\sqrt{x}\left(\sqrt{x}-1\right)+7\left(\sqrt{x}-1\right)=\left(\sqrt{x}-1\right)\left(7-3\sqrt{x}\right)\)
\(\left(1-a\right)\left(a+\sqrt{a}+1\right)\)