Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(MSC:45\)
\(\dfrac{1}{3}=\dfrac{15}{45}\); \(\dfrac{2}{15}=\dfrac{6}{45}\); \(\dfrac{4}{45}\) giữ nguyên
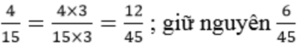
2/5 và 3/7
2/5=14/35 ; 3/7=15/35
4/15 va 6/45
4/15 = 12/45 ; giữ nguyên phân số 6/45
\(\frac{1}{3};\frac{2}{15};\frac{4}{45}\)
Ta có : Mẫu số chung là 45 vì \(45\) \(⋮3;15\)
\(\frac{1}{3}=\frac{1.15}{3.15}=\frac{15}{45}\)
\(\frac{2}{15}=\frac{2.3}{15.3}=\frac{6}{45}\)
Còn \(\frac{4}{45}\)ta giữ nguyên.
2/5 và 3/7 thành 14/35 và 15/35
4/15 và 6/45 thành 12/45 và 6/45
1/2, 1/5 và 1/3 thành 15/30, 6/30 và 10/30.
\(\dfrac{11}{12}=\dfrac{11.4}{12.4}=\dfrac{44}{48}\) và \(\dfrac{7}{48}\)
\(\dfrac{61}{200};\dfrac{9}{50}=\dfrac{9.4}{50.4}=\dfrac{36}{200}\)
\(\dfrac{1}{3}=\dfrac{1.15}{3.15}=\dfrac{15}{45}\); \(\dfrac{2}{15}=\dfrac{2.3}{15.3}=\dfrac{6}{45}\) và 4/45
Mẫu số chung nhỏ nhất là: 90
Mẫu số chung nhỏ nhất chính là bội chung nhỏ nhất của 3 số: 45, 15, 30
Note: Trong số học, bội số chung nhỏ nhất (hay còn gọi tắt là bội chung nhỏ nhất, viết tắt là BCNN, tiếng Anh: least common multiple hoặc lowest common multiple (lcm) hoặc smallest common multiple) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho cả a vàb. Tức là nó có thể chia cho a và b mà không để lại số dư. Nếu a hoặc b là 0, thì không tồn tại số nguyên dương chia hết cho a và b, khi đó quy ước rằng LCM(a, b) là 0.
Bội số chung của 2 số a và b được kí hiệu là [a,b], BCNN(a,b) hoặc LCM(a,b).
Ví dụ: Bội của 4 là:
0,4,8,12,16,20,24,28,32,36,40,44....(thêm 4 để được bội số tiếp theo).
Bội của 6 là:
0,6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78,...
(thêm 6 để được bội số tiếp theo).
Bội chung của 4 và 6 là các số cùng xuất hiện trong hai dãy trên: 12, 24, 36, 48,....
Vậy bội chung nhỏ nhất của 4 và 6 là 12
Còn cách tìm cụ thể thì xem SGK toán 6
\(\frac{2}{5}\)=\(\frac{14}{35}\); \(\frac{4}{7}\)=\(\frac{20}{35}\)
\(\frac{4}{15}\)=\(\frac{12}{45}\);giữ nguyên phân số \(\frac{6}{45}\)
\(\frac{1}{2}\)=\(\frac{15}{30}\);\(\frac{1}{5}\)=\(\frac{6}{30}\);\(\frac{1}{3}\)=\(\frac{10}{30}\)
theo thứ tự nha
14/35 và 20/35
12/45 và 6/45 hoặc 4/15 và 2/15
15/30;6/30;10/30
\(a.\dfrac{3}{4}=\dfrac{3.9}{4.9}=\dfrac{27}{36}\)
\(\dfrac{5}{9}=\dfrac{5.4}{9.4}=\dfrac{20}{36}\)
\(b.\dfrac{5}{6}=\dfrac{5.3}{6.3}=\dfrac{15}{18}\) giữ nguyên phân số còn lại
c. \(\dfrac{3}{8}=\dfrac{3.3}{8.3}=\dfrac{9}{24}\)
\(\dfrac{7}{12}=\dfrac{7.2}{12.2}=\dfrac{14}{24}\)
d. \(\dfrac{11}{12}=\dfrac{11.4}{12.4}=\dfrac{44}{48}\)
giữ nguyên phân số còn lại.
e. \(\dfrac{9}{50}=\dfrac{9.4}{50.4}=\dfrac{36}{200}\)
giữ nguyên phân số còn lại
\(f.\dfrac{1}{3}=\dfrac{1.3}{15.3}=\dfrac{3}{45}\)
\(\dfrac{2}{15}=\dfrac{2.3}{15.3}=\dfrac{6}{45}\)
giữ nguyên phân số còn lại
Bài 3 :
a: \(MSC:12\\ \dfrac{4}{3}=\dfrac{4\times4}{3\times4}=\dfrac{16}{12};\dfrac{3}{4}=\dfrac{3\times3}{3\times4}=\dfrac{9}{12}\)
b: \(MSC:12\\ \dfrac{5}{4}=\dfrac{5\times3}{4\times3}=\dfrac{15}{12};\dfrac{5}{6}=\dfrac{5\times2}{6\times2}=\dfrac{10}{12}\)
c:\(MSC:24\\ \dfrac{3}{8}=\dfrac{3\times3}{8\times3}=\dfrac{9}{24};\dfrac{1}{6}=\dfrac{1\times2}{6\times2}=\dfrac{2}{12}\)
d: \(MSC:35\\ \dfrac{2}{5}=\dfrac{2\times7}{5\times7}=\dfrac{14}{35};\dfrac{4}{7}=\dfrac{4\times5}{7\times5}=\dfrac{20}{35}\)
Bài 3:
a: 4/3=16/12
3/4=9/12
b: 5/4=30/24
5/6=20/24
c: 3/8=18/48
1/6=8/48
d: 2/5=14/35
4/7=20/35
Bài 4:
a: 7/12=28/48
5/48=5/48
b: 4/100=4/100
8/25=32/100
\(a,\dfrac{1}{4},\dfrac{5}{6}và\dfrac{7}{12}\)
\(\dfrac{1}{4}=\dfrac{1\times3}{4\times3}=\dfrac{3}{12};\dfrac{5}{6}=\dfrac{5\times2}{6\times2}=\dfrac{10}{12};\dfrac{7}{12}\)
\(b,\dfrac{1}{9},\dfrac{3}{5},\dfrac{11}{45}\)
\(\dfrac{1}{9}=\dfrac{1\times5}{9\times5}=\dfrac{5}{45};\dfrac{3}{5}=\dfrac{3\times9}{5\times9}=\dfrac{27}{45};\dfrac{11}{45}\)
