Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

Bài 1: Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
\(\Rightarrow\)\(FG//AD\)
C/m tương tự đc \(EH//AD; GH//EF//BC\)
\(\Rightarrow EFGH\) là hình bình hành
a/Để EFGH là hình chữ nhật thì góc \(FGH=90^o\)
\(\Rightarrow góc HGD+góc FGC=90^o\)
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
\(\Rightarrow\) góc BCD+góc ADC=\(90^o\)
\(\Rightarrow\)Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=\(90^o\)
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
\(\Rightarrow\)AD=BC
\(\Rightarrow\)Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi\(\Rightarrow \)ABCD phải có đủ cả 2 điều kiện trên

Xét \(\Delta ABC\)có:
DB = DA (giả thiết)
AE = CE (giả thiết)
\(\Rightarrow DE\)là đường trung bình của \(\Delta ABC\)
\(DE//BC\)(tính chất) \(\Rightarrow DE//BF\)(1)
Và \(2DE=BC\)(tính chất)
Mà \(2BF=BC\)(vì \(BF=CF\))
\(\Rightarrow2DE=2BF\Rightarrow DE=BF\)(2)
Xét tứ giác BDEF có: (1) và (2).
\(\Rightarrow BDEF\)là hình bình hành.
Vậy BDEF là hình bình hành.

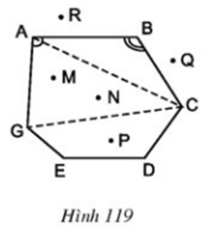
Các đỉnh là các điểm: A, B, C, D, E, G
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc C và D, hoặc D và E, hoặc E và G, hoặc G và A
Các cạnh là các đoạn thẳng: AB, BC, CD, DE, EG, GA
Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, AD, AE, BG, BE, BD, CE, DG
Các góc là: ∠A , ∠B , ∠C , ∠D , ∠E , ∠G
Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, P
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, R

A B C D M N I K
nối BD và AC
trong tam giác ABC ta có: M và N lần luợt là trung đỉêm của AB và AC
=> MN là đuờng trung bình của tam giác ABC
=> MN//AC(
trong tam giác ADC ta có I và K lần luợt là trung điểm của DC và DA
=> KI là đuờng trung bình của tam giác ADC
=> KI//AC
ta có: KI//AC
MN//AC
=> KI//MN(1)
trong tam giác ABD có M và K lần luợt là trung điểm của AB và AD
=> MK là đuờng trung bình của tam giác ADB
=> MK//DB
trong tam giác CDB có I và N lần luợt là trung điểm của DC và CB
=> IN là đuờng trung bình của tam, giác CDB
=>IN//BD
ta có: MK//DB
IN//DB
=> MK//IN(2)
từ (1)(2)=> MK//IN
MN//KI
=> MNIK là hình bình hành
Bài 1:Vẽ đường chéo BD
Xét tam giác ADB có:
M là trung điểm của AB
K là trung điểm của AD
=>KM là đường trung bình của tam giác ADB
=>KM//DB(1) và KM=1/2 DB(3)
Xét tam giác BCD có:
N là trung điểm của BC
I là trung điểm của DC
=>NI là đường trung bình của tam giác BCD
=>NI//DB(2) và NI=1/2DB(4)
Từ (1) và (2)=>KM//NI( //DB)(5)
Từ (3) và (4)=>KM=NI(=1/2 DB)(6)
Từ (5) và (6)=>KMNI là hình bình hành (dhnb3)

* Hướng dẫn câu b:
Gọi I là giao điểm của Gx và PQ. Kéo dài PQ cắt hai cạnh AD và BC theo thứ tự là E và F.
Góc MPQ = góc GEF (so le trong do MP // AD)
Góc MQP = góc GFE (so le trong do MQ // BC)
góc MPQ = góc MQP (tam giác MPQ cân do MP = MQ)
=> góc GEF = góc GEF -> tam giác GEF cân tại G
mà GI là phân giác của góc G -> GI vuông góc với EF
-> Gx vuông góc với PQ -> Gx // MN (MN vuông góc với PQ do hình thoi có 2 đường chéo vuông góc).
Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
Ví dụ :
B(5) = {5.1, 4.2, 5.3, …} = {5, 10, 15, …}
Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
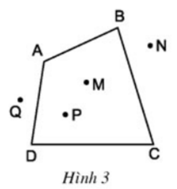


a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A
Hai đỉnh đối nhau: A và C, B và D
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD
c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB
Hai cạnh đối nhau: AB và CD, AD và BC
d) Góc: ∠A , ∠B , ∠C , ∠D
Hai góc đối nhau: ∠A và ∠C , ∠B và ∠D
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q