Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
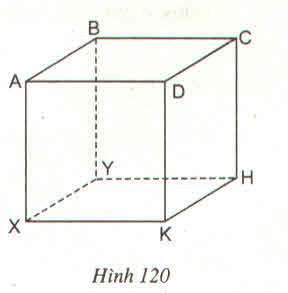
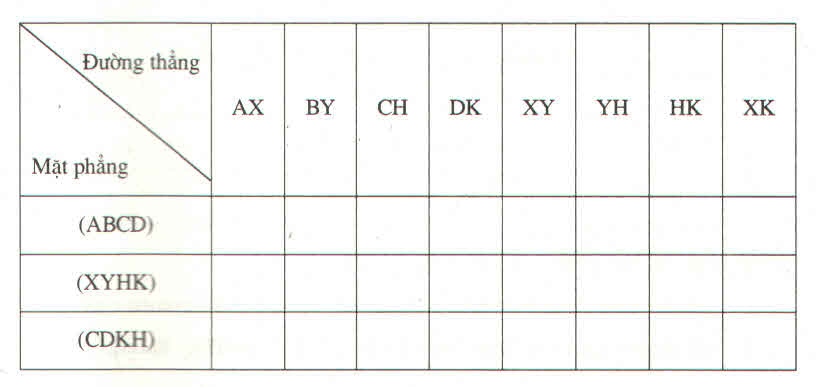
a. Những cặp mặt phẳng song song với nhau là:
mp (ABCD) và mp (XYHK)
mp (ADKX) và mp (BCHY)
mp (ABYX) và mp (CDKH)
b. Những cặp mặt phẳng vuông góc với nhau là:
mp (ABCD) và mp (ADKX); mp (XYHK) và mp (ADKX)
mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)
mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)
mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)
mp (ADKX) và mp (CDKH); mp (ADKX) và mp (ABYX)
mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)
c. Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau.
d: 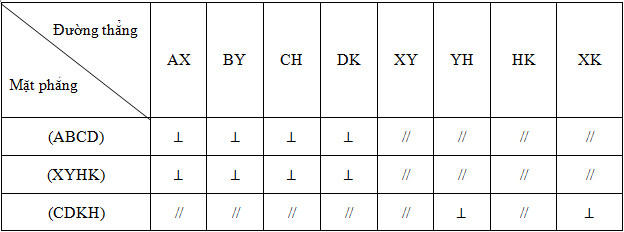

Lời giải
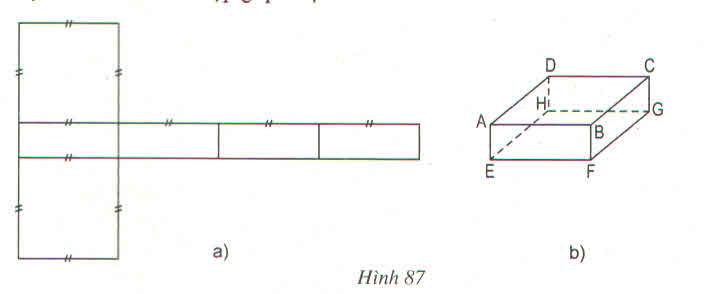
1. Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và (DHEA)
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H.
1. Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và (DHEA)
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H.

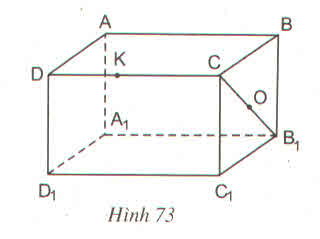
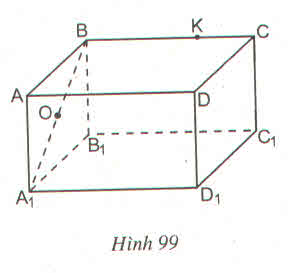
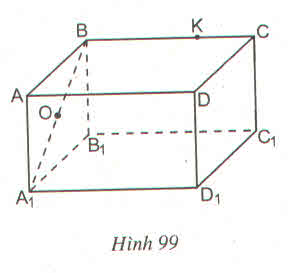
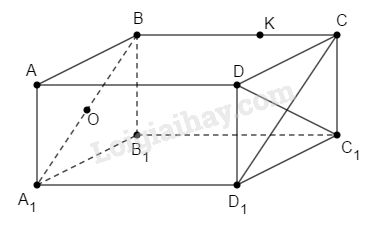
Với hình hộp chữ nhật ABCD. A 1B1C1D1
a) Nếu O là trung điểm của đoạn CB1 thì O cũng là trung điểm của đoạn C1B vì CBB1C1 là hình chữ nhật nên hai đường chéo có chung một trung điểm.
b) K là điểm thuộc cạnh CD thì K không thuộc cạnh BB1 vì bốn điểm C, D, B, B1 không thuộc một mặt phẳng

a) Câu trả lời trên là có. Thật vậy, vì mặt bên BCC1B1 là hình chữ nhật có O là trung điểm của đường chéo CB1 nên O cũng là trung điểm của đường chéo BC1 (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn BC1.
b) K không thuộc cạnh BB1 vì K ∉ mp( BB1C1C ) mà BB1 thuộc mặt phẳng đó
Vậy K không thuộc cạnh BB1.

A B C M D E 8 6
a) ADME là hình gì?
tứ giác ADME có:
\(\widehat{A}=90^o\)(Tam giác ABC vuông tại A)
\(\widehat{MDA}=90^o\)(\(MD\perp AB\))
\(\widehat{MEA}=90^o\)(\(ME\perp AC\))
Suy ra ADME là hình chữ nhật.
b) Tìm điều kiện của tam giác ABC để ADME là hình vuông
Hình chữ nhật ADME là hình vuông
\(\Leftrightarrow\)AM là phân giác \(\widehat{DAE}\)hay AM là phân giác \(\widehat{BAC}\)
mà AM là trung tuyến của tam giác vuông ABC
\(\Rightarrow\Delta ABC\)vuông cân tại A.
c) tính AM?
Áp dụng định lý pytago vào tam giác ABC
có \(BC^2=AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\left(cm\right)\)
Vì AM là đường trung tuyến ứng với cạnh huyền BC của tam giác vuông ABC nên \(AM=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\)
d) Tính \(S_{ABM}\)?
tam giác ABC có M trung điểm BC mà ME // AD (ADME hình chữ nhật) hay ME // AB
=> ME là đường trung bình tam giác ABC
=> E trung điểm AC
\(\Rightarrow AE=\frac{AC}{2}=\frac{6}{2}=3\left(cm\right)\)
mà DM = AE (ADME là hcn)
\(\Rightarrow AE=DM=3\left(cm\right)\)
\(\Rightarrow S_{ABM}=\frac{1}{2}.AB.DM=\frac{1}{2}.8.3=12\left(cm^2\right)\)
ĐS:...........
(Thời gian hoàn thành 9:37 PM)
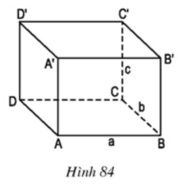

- A’A có vuông góc với AD vì là hai cạnh kề nhau của hình chữ nhật AA’D’D
- A’A có vuông góc với AB vì là hai cạnh kề nhau của hình chữ nhật AA’B’B