
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


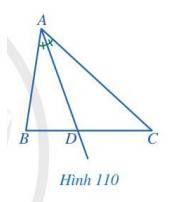
Các đầu mút của đoạn thẳng AD có đặc điểm: đầu mút A là đỉnh của tam giác, đầu mút D thuộc cạnh BC.

Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng

b: Gọi O là điểm nằm trên đường trung trực của AB
=>OH⊥AB tại H
=>H là trung điểm của AB
Xét ΔOHA vuông tại H và ΔOHB vuông tại H có
OH chung
HA=HB
Do đó: ΔOHA=ΔOHB
Suy ra: OA=OB

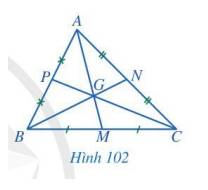
Ba đường trung tuyến AM, BN, CP của tam giác ABC có cùng đi qua một điểm là điểm G.

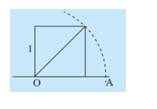
Đường chéo của hình vuông có độ dài đường chéo là 1 bằng \(\sqrt 2 \).
\(\sqrt 2 \) là số vô tỉ.
Lời giải:
Ta quan sát thấy hình vuông trong hình có độ dài cạnh là 1 nên độ dài đường chéo của nó là √22. Mặt khác, ta thấy độ dài đường chéo của hình vuông bằng độ dài cạnh OA. Do đó độ dài cạnh OA = √22.
Mà √22 không phải số hữ tỉ nên OA không phải số hữu tỉ.
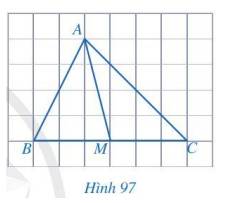
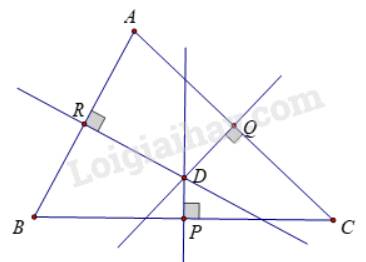
Các đầu mút của đoạn thẳng AM: đầu mút A là một đỉnh của tam giác, đầu mút M là trung điểm của cạnh BC trong tam giác ABC.