Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCD là hình vuông
\(\Rightarrow\Delta ABD\&\Delta ACD\) là tam vuông cân
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|.\sqrt[]{2}\\\left|\overrightarrow{BD}\right|=\left|\overrightarrow{AB}\right|.\sqrt[]{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\\\left|\overrightarrow{BD}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\end{matrix}\right.\)
\(\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.\left|\overrightarrow{AC}\right|\) (O là trung điểm AC)
\(\Rightarrow\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.1=\dfrac{1}{2}\)

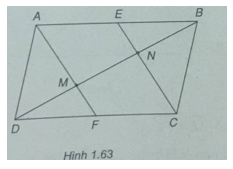
AECF là hình bình hành => EN // AM
E là trung điểm của AB => N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy →DM=→MN=→NB

16.8
4.8
11111111111111111111111111111111111111111111111111111111111111111111111111111111111
@huynhcaominhtu bạn ko bt thì thôi cò cần trả lời vớ vẩn như thế ko ?




