Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc \(\dfrac{\pi}{2}\)
Khoảng cách giữa hai điểm là 360cm= \(\dfrac{3\lambda}{2}\) nên hai điểm này dao động ngược pha nhau độ lệch pha của chúng là π
b) Sau 0,1s sóng truyền được khoảng cách là 0,1.330 = 33m = \(\dfrac{55\lambda}{4}\)
Độ lệch pha là \(\dfrac{3\pi}{4}\)

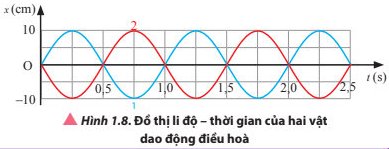
Hai dao động có cùng biên độ.
Ở cùng một thời điểm khi dao động 1 ở vị trí cân bằng thì dao động 2 ở vị trí bên và ngược lại.

Ta có: \(u=Acos\left(\dfrac{2\pi}{T}t-\dfrac{2\pi x}{\lambda}\right)\)
Khoảng cách giữa hai điểm gần nhau nhất dao động cùng pha là λ và khoảng cách giữa hai điểm gần nhau nhất dao động ngược pha là \(\dfrac{\lambda}{2}\)

Lời giải:
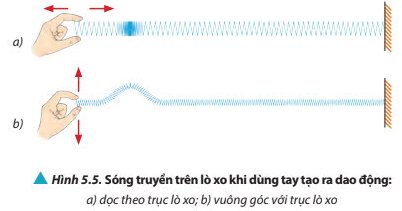
- Trường hợp a: phương truyền sóng và phương dao động của các điểm trên lò xo có phương trùng nhau.
- Trường hợp b: phương truyền sóng và phương dao động của các điểm trên lò xo có phương vuông góc với nhau.
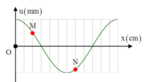
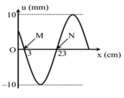

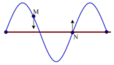

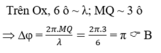
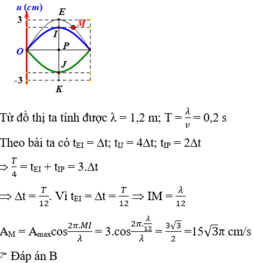
Vì: \(AB=\dfrac{\lambda}{4}\)
Độ lệch pha của hai điểm là:
\(\Delta\varphi=\dfrac{2\pi}{\lambda}AB=\dfrac{2\pi}{\lambda}\cdot\dfrac{\lambda}{4}=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\) rad