Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khi vật đi từ vị trí biên về vị trí cân bằng, thế năng của con lắc đơn giảm dần từ giá trị cực đại (bằng cơ năng của con lắc) về 0 (Mốc thế năng tại vị trí cân bằng). Do cơ năng của con lắc được bảo toàn, tổng của động năng và thế năng không đổi nên thế năng giảm bao nhiêu, động năng tăng bấy nhiêu. Do đó, khi vật đi từ biên về vị trí cân bằng, động năng của vật tăng từ 0 đến cực đại.
- Khi vật đi từ vị trí cân bằng về vị trí biên, thế năng của con lắc tăng dần từ 0 đến cực đại, trong khi động năng giảm dần từ cực đại về 0.

Tham khảo:
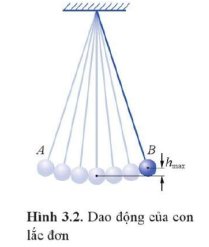
Tại vị trí A : Khi con lắc tiếp tục di chuyển từ vị trí cân bằng sang vị trí biên A, tốc độ của nó giảm dần làm cho động năng giảm dần. Đồng thời, độ cao của vật tăng dần làm cho thế năng của nó tăng dần.
Khi quả cầu đi qua vị trí cân bằng O: Lúc này, động năng của con lắc đơn lớn nhất và thế năng bằng 0. Vật treo ở vị trí thấp nhất và chuyển hướng đi ngược lại.
Tại vị trí B: Khi con lắc di chuyển từ vị trí biên B vào vị trí cân bằng O, tốc độ của vật tăng dần làm cho động năng của nó tăng dần. Trong khi đó, độ cao của vật giảm dần làm cho thế năng của nó giảm dần.

Công thức (3.5): \(W_d=\dfrac{1}{2}mw^2A^2sin^2\left(wt+\varphi_0\right)\)
Đồ thị động năng – thời gian cũng có dạng hình sin.
Từ đồ thị ta thấy:
+ Tại thời điểm ban đầu, động năng bằng 0
+ Tại thời điểm \(\dfrac{T}{4}\), động năng cực đại
+ Tại thời điểm \(\dfrac{T}{2}\), động năng bằng 0
+ Tại thời điểm \(\dfrac{3T}{4}\), động năng cực đại
+ Tại thời điểm T, động năng bằng 0.

Khi thế năng của vật tăng thì động năng của vật giảm và cơ năng luôn bằng tổng giá trị của động năng và thế năng .

a. Dựa vào đồ thị ta có:
Chu kì \(T = 2 s\), suy ra tần số góc \(\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2} = \pi\) rad/s
Vận tốc cực đại của dao động: \(\text{v}_{m a x} = \omega A\)
\(\Rightarrow A = \frac{\text{v}_{m a x}}{\omega} = \frac{4}{\pi}\) cm
Thời điểm \(t = 0\), vật có \(\text{v} = \text{v}_{m a x}\), suy ra vật ở VTCB và \(\text{v} > 0\)
Khi đó: \(x = 0 \Rightarrow cos \varphi = 0 \Rightarrow \varphi = - \frac{\pi}{2}\)
Phương trình của vận tốc có dạng: \(\text{v} = \omega A cos \left(\right. \omega t + \varphi + \frac{\pi}{2} \left.\right)\)
\(\Rightarrow \text{v} = 4 cos \left(\right. \pi t - \frac{\pi}{2} + \frac{\pi}{2} \left.\right) = 4 cos \left(\right. \pi t \left.\right)\) (cm/s)
b. Phương trình dao động điều hòa có dạng: \(x = A cos \left(\right. \omega t + \varphi \left.\right)\)
\(\Rightarrow x = \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} \left.\right)\) (cm)
Phương trình của gia tốc có dạng: \(a = \omega^{2} A cos \left(\right. \omega t + \varphi + \pi \left.\right)\)
\(\Rightarrow a = \pi^{2} . \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} + \pi \left.\right) = 4 \pi cos \left(\right. \pi t + \frac{\pi}{2} \left.\right)\) (cm/s2)

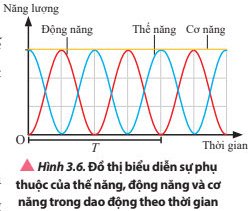
a) Từ 0 đến \(\frac{T}{4}\): Wđ tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{4}\), Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{4}\).
Từ \(\frac{T}{4}\)đến \(\frac{T}{2}\): Wđ giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{2}\), Wt tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{2}\).
Từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\): Wđ tăng từ 0 đạt giá trị lớn nhất tại \(\frac{{3T}}{4}\),Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{{3T}}{4}\).
Từ \(\frac{{3T}}{4}\)đến T: Wđ giảm từ giá trị lớn nhất về 0 tại T, Wt tăng từ 0 đến giá trị lớn nhất tại T.
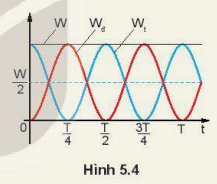
b) Tại thời điểm t = 0: Wđ = 0, Wt = W.
Tại thời điểm t = \(\frac{T}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
Tại thời điểm t = \(\frac{T}{4}\): Wđ = W, Wt = 0.
Tại thời điểm t = \(\frac{{3T}}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
→ ở mỗi thời điểm trên ta đều có: Wđ + Wt = W.
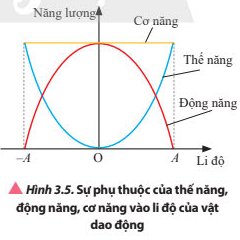
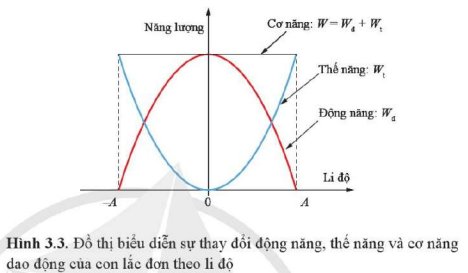



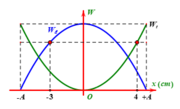
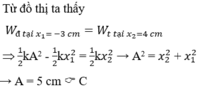
Vật chuyển động từ biên âm về vị trí cân bằng thì thế năng của vật giảm từ giá trí lớn nhất về 0 còn động năng thì tăng dần từ 0 đến giá trị lớn nhất và ngược lại.
Vật chuyển động từ vị trí cân bằng đến vị trí biên âm thì thế năng của vật tăng dần từ 0 đến giá trị lớn nhất còn động năng giảm dần từ giá trị lớn nhất về 0 và ngược lại.