Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
Trong nhiệt giai Ken-vin, công thức của định luật Sác-lơ là: p T = hằng số.
→ phát biểu (1), (3) đúng, phát biểu (2) sai vì từ 200oC lên 400oC tương ứng với 473K lên 673K, không tăng gấp đôi được.
Đường đẳng tích (p, T) là nửa đường thẳng có đường kéo dài đi qua gốc tọa độ → (4) đúng.

Trạng thái 1: \(\left\{{}\begin{matrix}p_1=1atm\\V_1=10l\\T_1=27^oC=300K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=2atm\\V_2=15l\\T_2=???\end{matrix}\right.\)
Quá trình khí lí tưởng:
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Rightarrow\dfrac{1\cdot10}{300}=\dfrac{2\cdot15}{T_2}\)
\(\Rightarrow T_2=900K=627^oC\)

Tóm tắt đề bài như sau:
\(\left\{{}\begin{matrix}V=10\left(l\right)\\p=2\left(atm\right)\\T=87+273=360\left(K\right)\end{matrix}\right.\underrightarrow{Đẳngáp}\left\{{}\begin{matrix}V_1=?\\p_1=2\left(atm\right)\\T_1=\dfrac{T}{2}=180\left(K\right)\end{matrix}\right.\) \(\underrightarrow{Đẳngnhiet}\left\{{}\begin{matrix}V_2=?\\p_2=0,5\left(atm\right)\\T_2=180\left(K\right)\end{matrix}\right.\)
Phương trình trạng thái khí lí tưởng ( Claperon Mendeleep ): \(\dfrac{pV}{T}=const\)
Đẳng áp: \(\dfrac{V}{T}=\dfrac{V_1}{T_1}\Leftrightarrow V_1=\dfrac{10.180}{360}=5\left(l\right)\)
Đẳng nhiệt: \(p_1V_1=p_2V_2\Rightarrow V_2=\dfrac{p_1V_1}{p_2}=\dfrac{2.5}{0,5}=20\left(l\right)\)
Vậy thể tích sau cùng của khối khí trên là V2=20(l)

\(T_1=27^oC=300K\)
Quá trình khí lí tưởng:
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\)
\(\Rightarrow\dfrac{1\cdot10}{300}=\dfrac{15\cdot2\cdot1}{T_2}\)
\(\Rightarrow T_2=900K=627^oC\)
Cho em hỏi ạ ⇒1.10/300=15.2.1 /T ngay chỗ 15.2.1 số 1 ơn đâu mà nhân vào ạ

Đồ thị được biểu diễn trên hình 122
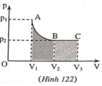
Nhận xét: Diện tích hình A V 1 V 2 B (phần gạch chéo) lớn hơn diện tích hình B V 2 V 3 C (phần nét chấm) nên công trong quá trình đẳng nhiệt ( A → B ) lớn hơn công trong quá trình đẳng áp ( B → C ).

Khoan? sao đề lại hỏi nhiệt độ sau cùng chẳng phải đã biết nhiệt độ sau cùng rồi sao???
\(\left\{{}\begin{matrix}V=10\left(l\right)\\p=0,8\left(atm\right)\\T=27+273=300\left(K\right)\end{matrix}\right.\underrightarrow{Đẳngtích}\left\{{}\begin{matrix}V_1=10\left(l\right)\\p_1=?\\T_1=T+300=600\left(K\right)\end{matrix}\right.\) \(\underrightarrow{Đẳngnhiet}\left\{{}\begin{matrix}V_2=25\left(l\right)\\p_2=?\\T_2=600\left(K\right)\end{matrix}\right.\)
Đáp án: A
Từ phương trình trạng thái ta được:
Để p tỷ lệ với số phân tử chứa trong một đơn vị thể tích (n) thì T phải không đổi
→ quá trình biến đổi là đẳng nhiệt.