Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔBAD có EF//AD
nên EF/AD=BF/BA=BE/BD
Xét ΔBDC có GE//DC
nên BG/BC=BE/BD
=>BG/BC=BF/BA
=>FG//AC
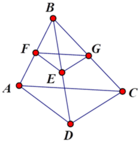
qua điểm E thuộc đg chéo BD của tgiac ABCD, vẽ EF//AD( F thuộc AB), EG//DC( G thuộc BC). cm: FG //AC


Áp dụng định lý Ta-lét trong ΔABD với EF // AD, ta có B E E D = B F F A (1)
Áp dụng định lý Ta-lét trong ΔBDC với EG // DC, ta có B E E D = B G G C (2)
Từ (1) và (2) suy ra B F F A = B G G C , do đó FG // AC (định lý Ta-lét đảo)
Vậy A, B, C đúng, D sai
Đáp án: D

\(\frac{AE}{DE}=\frac{AF}{CF}\left(1\right)\) EF//DC, \(\frac{AG}{BG}=\frac{AF}{CF}\left(2\right)\) FG//BC
(1) (2)\(\Rightarrow\frac{AE}{DE}=\frac{AG}{BG}\Rightarrow AE.BG=DE.AG\) Sai đề

b: Xét tứ giác AEPF có
AE//PF
AF//PE
góc FAE=90 độ
=>AEPF là hcn
=>góc AEF=góc APF=góc ADB
=>FE//BD
Có: EF//AD \(\Rightarrow\dfrac{BF}{FA}=\dfrac{BE}{ED}\)(Đ.lí Ta-lét)
Có: EG//CD\(\Rightarrow\dfrac{BG}{GC}=\dfrac{BE}{ED}\)(Đ.lí Ta-lét)
\(\Rightarrow\dfrac{BF}{FA}=\dfrac{BG}{GC}\)\(\Rightarrow\)FG//AC