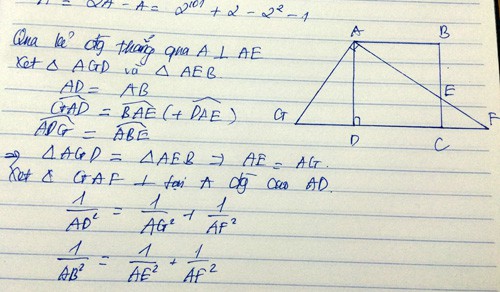Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ AG⊥AF
Xét △ABE và △ADG có
\(\widehat{BAE}=\widehat{DAG}\) (cùng phụ góc DAF)
\(\widehat{ABE}=\widehat{ADG}=90^o\)
suy ra △ABE=△ADG
=> AE=AG(2 cạnh tương ứng)
Xét △AGF vuông tại A đường cao AD, Ta có:
\(\dfrac{1}{AD^2}=\dfrac{1}{AG^2}+\dfrac{1}{AF^2}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)

Vẽ thêm đường thẳng AN vuông góc với AM và cắt CD ở N. Chứng minh được: \(\Delta AND=\Delta AMB\left(c-g-c\right)\Rightarrow AM=AN\)(cạnh tương ứng)
Tiếp tục áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ANI .......... => ĐPCM

A B C D M I E
Từ A kẻ AE vuông góc với AI , cắt CD ở E.
Xét hai tam giác vuông : tam giác EAD và tam giác ABM có AD = AB = a
góc EAD = góc BAM vì cùng phụ với góc DAI
=> tam giác DAF = tam giác BAM (cgv.gnk) => AE = AM
áp dụng hệ thức về cạnh trong tam giác vuông AEI có đường cao AD ứng với cạnh huyền EI :
\(\frac{1}{AD^2}=\frac{1}{AE^2}+\frac{1}{AI^2}\) hay \(\frac{1}{AM^2}+\frac{1}{AI^2}=\frac{1}{a^2}\)

Hình bạn tự vẽ nha.
a, ABCD là hình vuông \(\Rightarrow AB=BC=CD=AD\)
Ta có: \(\hat{IAD}+\hat{DAE}=90^o\)
\(\hat{BAE}+\hat{DAE}=90^o\)
\(\Rightarrow \hat{IAD} =\hat{BAE}\)
Xét \(\Delta ADI\) và \(\Delta ABE\) có:
\(\hat{ADI}=\hat{ABE}=90^o\)
\(AD=AB\left(cmt\right)\)
\(\hat{IAD}=\hat{BAE}(cmt)\)
\(\Rightarrow\Delta ADI=\Delta ABE\left(g-c-g\right)\Rightarrow AI=AE\)
b, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow AD.IK=AI.AK\) (hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow AD.IK=AE.AK\)
c, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AI^2}+\dfrac{1}{AK^2}\)(hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) mà hình vuông ABCD không đổi \(\Rightarrow\) AD không đổi\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi
Vậy \(\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi khi E thay đổi trên cạnh BC
Hai câu cuối í ẹ chưa nghĩ ra, để sau.