Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Con lắc đặt trong điện trg đều có phương ngang →\(\overrightarrow{P}\perp\overrightarrow{E}\) → g''=\(\sqrt{g^2+a^2}\) Ta có : F=qE=ma → a=2 m/s2 → g''=10 m/s2
T= 2π\(\sqrt{\frac{\Delta l}{g^{''}}}\) và khi buông nhẹ cho dao động thì ::A=\(\Delta l\) .Đế bài chép thiếu \(l\)rồi. lắp số vô là ok

- Góc lệch của dây treo VTCB:
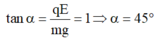
Gia tốc trong trường biểu kiến:
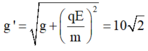
- Khi kéo lệch khỏi VTCB một góc 54° so với phương thẳng đứng thì α = 9° (góc lệch dây treo tại VTCB mới)
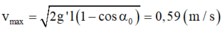

Đáp án A
Góc lệch của dây treo VTCB :
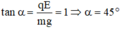
Gia tốc trong trường biểu kiến
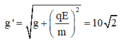
Khi kéo lệch khỏi VTCB một góc 54 ° so với phương thẳng đứng thì
![]() (góc lệch dây treo tại VTCB mới)
(góc lệch dây treo tại VTCB mới)
![]()

Giải thích: Đáp án C
Phương pháp: Sử dụng lí thuyết về con lắc đơn chịu tác dụng của ngoại lực
Cách giải:
VTCB mới của con lắc là VT mà dây treo hợp với phương thẳng đứng góc β sao cho: 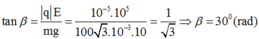
Kéo con lắc đơn ra khỏi phương thẳng đứng góc 600 rồi thả nhẹ => CLĐ sẽ dao động với biên độ α0=300.
Gia tốc trọng trường hiệu dụng 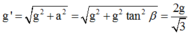
Lực căng dây cực đại của con lắc đơn: 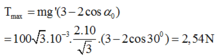
=> Chọn C
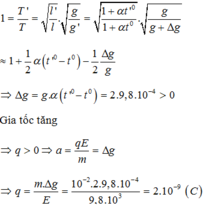


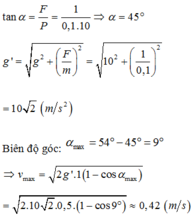

Chọn B
+ Khi con lắc ở VTCB mới O’ dây treo hợp với phương
thẳng đứng góc α0:
=> Lực căng cực đại của dây trong quá trình dao động là:
T = mg’(3 – 2cosα0 ) = 0,1.10,002(3 – 2cos(0,2012rad)) = 1,0406 N = 1,04N.