Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
- Chọn mốc thế năng hấp dẫn là vị trí va chạm
- Xét thời điểm ngay khi va chạm đàn hồi giữa m và M là hệ kín
- Áp dụmg định luật bảo toàn động lượng và cơ năng cho hệ ta có
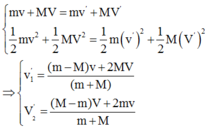
- Thay số ta được vận tốc của M ngay sau va chạm là:
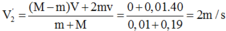
Bảo toàn cơ năng cho con lắc M gắn dây, sau khi va chạm vật M chuyển động lên đến vị trí dây treo lệch
với phương thẳng đứng một góc lớn nhất ứng với thế năng lớn nhất động năng bằng không vậy ta có:
![]()

Bài 1: Chọn chiều dương là chiều chuyển động của vật 1.
Vận tốc của vật 1 sau va chạm là:
\(v_1'=\frac{\left(m_1-m_2\right).v_1+2m_2.v_2}{m_1+m_2}=\frac{\left(2-1\right).4+2.1.\left(-6\right)}{2+1}=-\frac{8}{3}\left(m/s\right)\)
(dấu trừ thể hiện sau va chạm vật 1 chuyển động ngược chiều dương đã chọn).
Vận tốc của vật 2 sau va chạm là:
\(v_2'=\frac{\left(m_2-m_1\right).v_2+2.m_1.v_1}{m_1+m_2}=\frac{\left(1-2\right).\left(-6\right)+2.2.4}{2+1}=\frac{22}{3}\left(m/s\right)\)
Vậy:...

Lời giải
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của hai vật
Gọi v 1 , v 2 , V lần lượt là vận tốc của quả cầu 1, quả cầu 2 và hai quả cầu sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 3 , 78 = 4.6 + 5. v 2 4 + 5 ⇔ v 2 = 2 m / s
Đáp án: A

Lời giải
Hai vật va chạm đàn hồi trực diện. Chọn chiều dương là chiều chuyển động của viên bi 1 nên vận tốc của viên bi 2 là: v 2 = − 2 m / s . Ta có:
v 1 ' = m 1 − m 2 v 1 + 2 m 2 v 2 m 1 + m 2 = 3 − 2 .1 − 2.2.2 3 + 2 = − 1 , 4 m / s
v 2 ' = m 2 − m 1 v 2 + 2 m 1 v 1 m 1 + m 2 = 2 − 3 . ( − 2 ) + 2.3.1 3 + 2 = 1 , 6 m / s
Đáp án: B
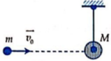

Gọi vận tốc sau va chạm lần lượt là \(v_1\) và \(v_2\).
Bảo toàn động lượng:
\(m_2v=m_1v_1+m_2v_2\)
\(\Rightarrow v_1+0,02v_2=1\left(1\right)\)
Bảo toàn năng lượng:
\(\frac{m_2v^2}{2}=\frac{m_1v^2_1}{2}+\frac{m_2v^2_2}{2}\)
hay:
\(m_2v^2=m_1v^2_1+m_2v^2_2\)
\(\Rightarrow v^2_1+0,02v^2_2=50\left(2\right)\)
Giải (1) và (2):
\(v_1=2,96\left(m\text{/}s\right)\)
\(v_2=-48\left(m\text{/}s\right)\)
Góc lệch cực đại \(\alpha\) dễ dàng đc tính theo công thức:
\(m_1gl\left(1-\cos\alpha\right)=\frac{m_1v^2_1}{2}\)
\(\alpha=65^0\)
có thể giải thích kĩ hơn ở pt (2) ko ạ??