Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\orbr{\begin{cases}2x+\frac{\pi}{6}=x+k2\pi\\2x+\frac{\pi}{6}=\pi-x+k2\pi\end{cases}}\) \(\Rightarrow\orbr{\begin{cases}x=-\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{18}+\frac{k2\pi}{3}\end{cases}}\)

1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+=???
Phép tính như thế thì mời nhà toán hok về lm giùm!
KO NÊN ĐĂNG CÂU HỎI LINH TINH!
#Biinz_Tổng's
#Dương_Hoàng_Anh

Chọn C.
Ta có: f(-1) = 1 và ![]()
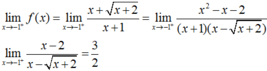
Suy ra ![]()
Vậy hàm số không liên tục tại x0 = -1.


\(y=\dfrac{1}{2x^2+x-1}=\dfrac{1}{\left(x+1\right)\left(2x-1\right)}=\dfrac{2}{3}.\dfrac{1}{2x-1}-\dfrac{1}{3}.\dfrac{1}{x+1}\)
\(y'=\dfrac{2}{3}.\dfrac{-2}{\left(2x-1\right)^2}-\dfrac{1}{3}.\dfrac{-1}{\left(x+1\right)^2}=\dfrac{2}{3}.\dfrac{\left(-1\right)^1.2^1.1!}{\left(2x-1\right)^2}-\dfrac{1}{3}.\dfrac{\left(-1\right)^1.1!}{\left(x+1\right)^2}\)
\(y''=\dfrac{2}{3}.\dfrac{\left(-1\right)^2.2^2.2!}{\left(2x-1\right)^3}-\dfrac{1}{3}.\dfrac{\left(-1\right)^2.2!}{\left(x+1\right)^3}\)
\(\Rightarrow y^{\left(n\right)}=\dfrac{2}{3}.\dfrac{\left(-1\right)^n.2^n.n!}{\left(2x-1\right)^{n+1}}-\dfrac{1}{3}.\dfrac{\left(-1\right)^n.n!}{\left(x+1\right)^{n+1}}\)
\(\Rightarrow y^{\left(2019\right)}=\dfrac{2}{3}.\dfrac{\left(-1\right)^{2019}.2^{2019}.2019!}{\left(2x-1\right)^{2020}}-\dfrac{1}{3}.\dfrac{\left(-1\right)^{2019}.2019!}{\left(x+1\right)^{2020}}\)
\(=\dfrac{2019!}{3}\left(\dfrac{1}{\left(x+1\right)^{2020}}-\dfrac{2^{2020}}{\left(2x-1\right)^{2020}}\right)\)

\(\left(2x+1\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k2^k.x^k\)
\(k\ge8\Rightarrow\) tổng hệ số
\(C_{10}^82^8+C_{10}^92^9+C_{10}^{10}2^{10}=45.2^8+10.2^9+2^{10}\)
\(=2^8\left(45+10.2+2^2\right)=69.2^8\)

Ta có : f − 1 = 1 và lim x → − 1 − f x = lim x → − 1 − ( 2 x + 3 ) = 2. ( − 1 ) + 3 = 1
lim x → − 1 + f x = lim x → − 1 + x + x + 2 x + 1 = lim x → − 1 + x 2 − x − 2 x + 1 x − x + 2 = lim x → − 1 + x − 2 x − x + 2 = 3 2
Suy ra : lim x → − 1 + f x ≠ lim x → − 1 − f x
Vậy hàm số gián đoạn tại x= -1.
Chọn đáp án C
kjho qua