KV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
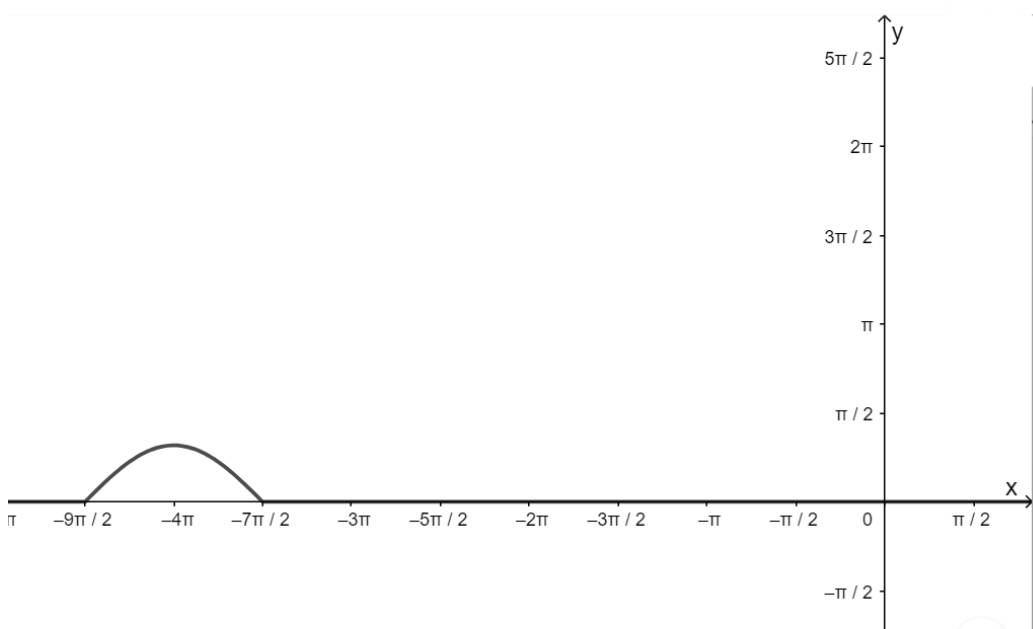
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
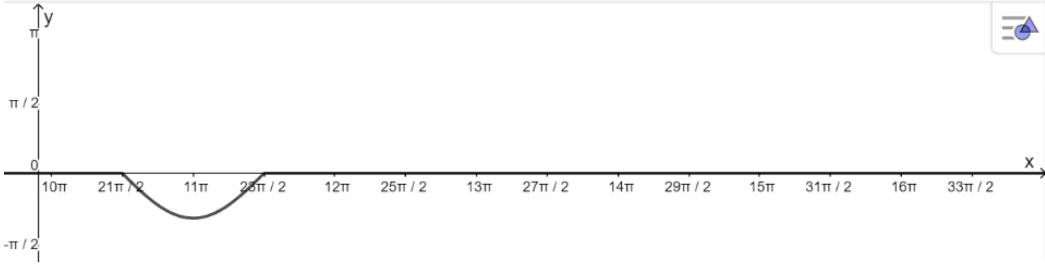
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
8 tháng 9 2021
Trên \(\left(-\dfrac{\pi}{2}+k.2\pi;\dfrac{\pi}{2}+k.2\pi\right)\) chọn 2 giá trị của x (x1 và x2) sao cho x1 > x2
Xét f(x1) - f(x2) = sinx1 - sinx2
= 2cos\(\dfrac{x_1+x_2}{2}\) . sin \(\dfrac{x_1-x_2}{2}\)
Do \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)
⇒ cos\(\dfrac{x_1+x_2}{2}\) > 0
Mà \(sin\dfrac{x_1-x_2}{2}\) > 0
nên f(x1) - f(x2) > 0
Vậy đồng biến
Nghịch biến tương tự
8 tháng 9 2021
tại sao \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)ạ ?
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2021
a.
\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)
b.
\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)
c.
\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)
NB
2
HT
27 tháng 9 2020
Biến đổi xong nó thành hàm nhìn gọn lắm :)
\(=\sin^6x+\cos^6x+\frac{3}{4}.\frac{1}{2}\left[\sin\left(2x+\frac{\pi}{4}-2x+\frac{\pi}{4}\right)+\sin\left(2x+\frac{\pi}{4}+2x-\frac{\pi}{4}\right)\right]\)
\(=1+\frac{3}{8}\left(\sin\frac{\pi}{4}+\sin4x\right)\)
Bạn biện luận nốt nhé
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 6 2021
\(y'=-2cos2x=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}\\x=\dfrac{\pi}{4}\end{matrix}\right.\)
BBT:
x y' y -pi/2 -pi/4 pi/4 pi/2 0 0 + - -
Hàm đồng biến trên \(\left(-\dfrac{\pi}{4};\dfrac{\pi}{4}\right)\) và nghịch biến trên các khoảng \(\left(-\dfrac{\pi}{2};-\dfrac{\pi}{4}\right);\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\)