Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lấy pt hoành độ giao điểm d và (P), ví dụ:
\(2x^2-5x+3=x+2\)
\(\Leftrightarrow2x^2-6x+1=0\)
Bấm máy pt này, nếu nó có nghiệm kép thì đấy là đáp án đúng
Kiểm tra thì D là đáp án đúng

a) Bảng biến thiên

Đồ thị hàm số
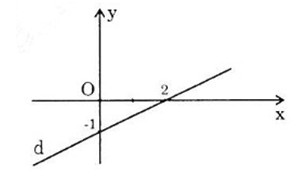
Đồ thị là đường thẳng đi qua 2 điểm:
+ Giao với trục tung P(0,-1)
+ Giao với trục hoành Q(2, 0)
b) Bảng biến thiên

Đồ thị hàm số
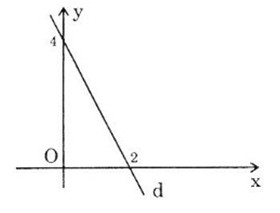
Đồ thị là đường thẳng đi qua 2 điểm:
+ Giao với trục tung P(0,4)
+ Giao với trục hoành Q(2, 0)
c) y=√x2y=x2 = |x| ={−x,x≤0x,x>0{−x,x≤0x,x>0
Bảng biến thiên
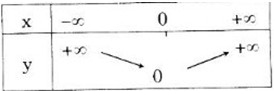
Đồ thị hàm số
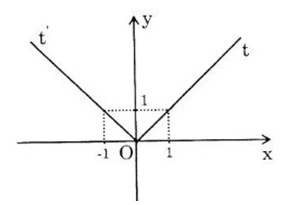
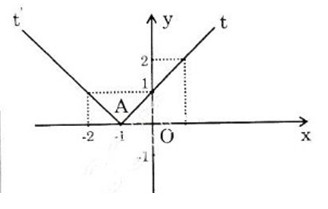
d) y = |x+1| = {−x−1,x≤−1x+1,x>−1{−x−1,x≤−1x+1,x>−1
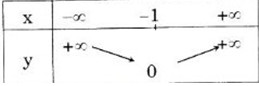
Bảng biến thiên
Đồ thị hàm số

a: ĐKXĐ: x^2-2x<>0 và x^2-1>0
=>(x>1 và x<>2) hoặc x<-1
b: ĐKXĐ: x+1>0 và 5-3x>0
=>x>-1 và 3x<5
=>-1<x<5/3
c: DKXĐ: 5x+3>=0 và 3-x>0
=>x>=-3/5 và x<3
=>-3/5<=x<3
d: ĐKXĐ: 4-x^2>0 và 1+x>=0
=>x^2<4 và x>=-1
=>-2<x<2 và x>=-1
=>-1<=x<2
e: ĐKXĐ: 2-3x<>0 và 1-6x>0
=>x<>2/3 và x<1/6
=>x<1/6

\(a.ĐKXĐ:\left\{{}\begin{matrix}\left|x\right|+4\ne0\\x-x^2\ge0\end{matrix}\right.\Leftrightarrow0\le x\le1\)
TXĐ : \(D=\left[0;1\right]\)
b. ĐKXĐ: \(\left|x-3\right|+\left|x+3\right|\ne0\)
Ta có : \(\left|x-3\right|+\left|x+3\right|\ge\left|x-3-x-3\right|=6>0\)
Nên hàm số xác định với mọi x
Tập xác định \(D=R\)
c. ĐKXĐ: \(\left\{{}\begin{matrix}\left|x\right|-1\ne0\\x^2-\left|x\right|\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\pm1\\\left|x\right|\left(\left|x\right|^3-1\right)\ge0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\\left|x\right|^3-1>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x>1\\x< -1\end{matrix}\right.\)
TXĐ : \(D=\left\{0\right\}U\left(-\infty;-1\right)U\left(1;+\infty\right)\)

a. Với $x_1, x_2\in\mathbb{R}$ thỏa $x_1\neq x_2$ thì:
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{-2(x_1^2-x_2^2)+(x_1-x_2)}{x_1-x_2}=1-2(x_1+x_2)\)
Với $x_1,x_2> \frac{1}{4}$ thì $A< 0$ nên hàm số nghịch biến trên $(\frac{1}{4}; +\infty)$
Với $x_1,x_2< \frac{1}{4}$ thì $A>0$ nên hàm số đồng biến trên $(-\infty; \frac{1}{4})$
b. TXĐ: $D=(-\infty; 2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2-x_1}-\sqrt{2-x_2}}{x_1-x_2}=\frac{-1}{\sqrt{2-x_1}+\sqrt{2-x_2}}< 0\)
Vậy hàm số nghịch biến trên tập xác định $(-\infty;2]$
c. TXĐ: $D=[0;2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2x_1-x_1^2}-\sqrt{2x_2-x_2^2}}{x_1-x_2}=\frac{2-(x_1+x_2)}{\sqrt{2x_1-x_1^2}+\sqrt{2x_2-x_2^2}}\)
Nếu $x_1,x_2\in (1;2)$ thì $A<0$ nên hàm số nghịch biến trên $(1;2)$
Nếu $x_1,x_2\in (0;1)$ thì $A>0$ nên hàm số nghịch biến trên $(0;1)$