Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta tính \(y'=3x^2-4x+1\)
\(y'=0\Rightarrow3x^2-4x+1=0\Rightarrow x=1;x=\frac{1}{3}\)
ta có
ta có trong khoảng 2 nghiệm thì y' cùng dấu với hệ số a, ngoài khoảng 2 nghiệm trái dấu với hệ số a
suy ra f'(x)>0 với \(x\in\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\) suy ra hàm số đồng biến trên \(\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\)
lại có f'(x)<0 với \(x\in\left(\frac{1}{3};1\right)\) suy ra hàm số nghịch biến trên \(\left(\frac{1}{3};1\right)\)

a) Hoành độ giao điểm của đồ thị hàm số \(y=\dfrac{2x+1}{2x-1}\) và \(y=x+2\) là nghiệm của phương trình :
\(\dfrac{2x+1}{2x-1}=x+2\Leftrightarrow\dfrac{2x+1}{2x-1}-x-2=0\)
\(\Leftrightarrow\dfrac{-2x^2-x+3}{2x-1}=0\)\(\Leftrightarrow\left\{{}\begin{matrix}-2x^2-x+3=0\\x\ne\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Với \(x=1\) thì \(y=1+2=3;x=-\dfrac{3}{2}\) thì \(y=-\dfrac{3}{2}+2=\dfrac{1}{2}\)
Vậy tọa độ hai giao điểm là \(A\left(1;3\right),B\left(-\dfrac{3}{2};\dfrac{1}{2}\right)\)

a) Tập xác định : R\ {1}; y′=−4(x−1)2<0,∀x≠1y′=−4(x−1)2<0,∀x≠1 ;
Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.
Bảng biến thiên :
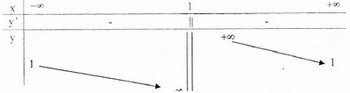
Đồ thị như hình bên. 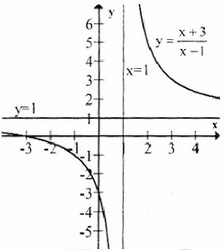
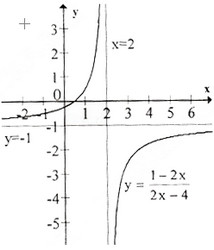
b) Tập xác định : R \{2}; y′=6(2x−4)2>0,∀x≠2y′=6(2x−4)2>0,∀x≠2
Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.
Bảng biến thiên :
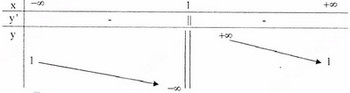
Đồ thị như hình bên.
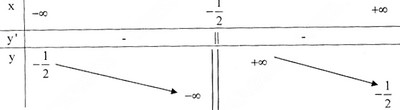
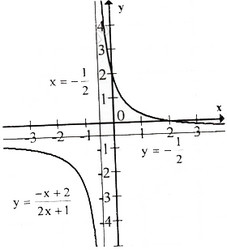
c) Tập xác định : R∖{−12}R∖{−12}; y′=−5(2x+1)2<0,∀x≠−12y′=−5(2x+1)2<0,∀x≠−12
Tiệm cận đứng : x=−12x=−12 . Tiệm cận ngang : y=−12y=−12.
Bảng biến thiên :
Đồ thị như hình bên.









Lời giải:
TXĐ: (-\infty; -1)\cup (-1;+\infty)$
$y'=\frac{1}{(x+1)^2}-2$
$y'>0\Leftrightarrow (x+1)^2< \frac{1}{2}\Leftrightarrow \frac{-1}{\sqrt{2}}-1< x< \frac{1}{\sqrt{2}}-1$
$y'< 0\Leftrightarrow (x+1)^2> \frac{1}{2}\Leftrightarrow x> \frac{1}{\sqrt{2}}-1$ hoặc $x< \frac{-1}{\sqrt{2}}-1$
Vậy hàm số:
Đồng biến trên $(\frac{-1}{\sqrt{2}}-1; \frac{1}{\sqrt{2}}-1)$ và nghịch biến trên $(\frac{1}{\sqrt{2}}-1; +\infty)\cup (-\infty; \frac{-1}{\sqrt{2}}-1)$