Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

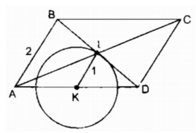
Gọi K là trung điểm của cạnh AD.
ta có AD cố định nên điểm K cố định.
Trong ∆ ABD ta có:
IB = ID (tính chất hình bình hành)
KA = KD (theo cách vẽ)
nên KI là đường trung bình của ∆ ABD
⇒ KI = 1/2 AB = 1/2.2 = 1 (cm) (tính chất đường trung bình của tam giác)
B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K; 1 cm)

A B C D O M N P Q
a/
Ta có
MN//AB (gt)
AD//BC=> AM//BN
=> AMNB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
AB//CD => AP//CQ mà AP = CQ (gt) => APCQ là hbh (Tứ giác có cặp cạnh đối // và = nhau là hbh)
b/
Xét hbh ABCD
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Xét hbh APCQ có
IA=IC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> \(I\equiv O\) (đều là trung điểm AC) => M; N; I thẳng hàng
c/ Do \(I\equiv O\) (cmt) => AC; MN; PQ đồng quy tại O

Kẻ IN, DM song song với BC
suy ra IN song song vs DM
Tam giác EDM có Itrung điểm DE và IN song song vs DM
suy ra In là đương trung binh của tam giác EDM
suy ra N là trung điểm Em
ta có DM song song với BC suy ra DMCB là hình thang
Mà góc ABC =ACB
nên DMCB là hình thang cân
suy ra DB =MC
ta lại có DB=AE
suy ra MC =AE
suy ra AE+EN=CM+MN
vậy AN=NC
VẬY N là trung điểm AC
Tam giác ACK có N là trung điểm AC và IN song song với BC
suy ra IN là đường trung bình tam giác AKB
suy ra I la trung điểm AK
tứ giác ADKE có I là trung điểm DE và I trung điểm AK
nêm ADKE là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường

A B C D E N F M I
a) - Xét \(\Delta AME\) và \(\Delta CNF\) có :
+ AM = CN (GT)
+ \(\widehat{MAE}=\widehat{NCF}\)(GT)
+ AE = CF ( GT )
=> \(\Delta AME=\Delta CNF\left(c.g.c\right)\) => ME = NF ( 2 cạnh tương ứng bằng nhau )
- Tương tự , \(\Delta DMF=\Delta BNE\left(c.g.c\right)\) => MF = NE ( 2 cạnh tương ứng bằng nhau )
- Xét tứ giác EMFN có :
+ ME = NF
+ MF = NE
=> EMFN là hình bình hành ( 2 cặp cạnh đối bằng nhau )
b) Vì ABCD là Hình bình hành => AC cắt BD tại I => I là trung điểm của AC , BD (1)
Tương tự AC cắt EF và MN tại trung điểm I của AC (2)
Từ 1 và 2 => EF và MN đều đi qua I

Gọi K là trung điểm của cạnh AD.
ta có AD cố định nên điểm K cố định.
Trong ∆ ABD ta có:
IB = ID (tính chất hình bình hành)
KA = KD (theo cách vẽ)
nên KI là đường trung bình của ∆ ABD
⇒ KI = \(\dfrac{1}{2}AB=\dfrac{1}{2}.2\) = 1 (cm) (tính chất đường trung bình của tam giác)
B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K ; 1 cm)