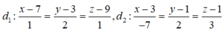Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 49\).
b) Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {2 - \left( { - 2} \right)} \right)}^2}} = 5\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)
c) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( { - 2;1} \right)\)
Bán kính đường tròn là: \[R = IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 3 - 1} \right)}^2}} = \sqrt {17} \]
Phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)
d) Bán kính đường tròn là: \(R = \frac{{\left| {1 + 2.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2}} }} = 2\sqrt 5 \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 20\)

a) Đường tròn (C) tâm \(O\left( {0;0} \right)\), bán kính \(R = 4\) có phương trình là: \({x^2} + {y^2} = 16\)
b) Đường tròn (C) tâm \(I\left( {2; - 2} \right)\), bán kính \(R = 8\) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y + 2} \right)^2} = 64\)
c) Gọi M, N lần lượt là trung điểm của AB, AC ta có: \(M\left( {\frac{1}{2};\frac{5}{2}} \right),N\left( {\frac{5}{2};\frac{7}{2}} \right)\)
Đường trung trực \(\Delta \)của đoạn thẳng AB là đường thẳng đi qua M và nhận vt \(\overrightarrow {BA} = (1;3)\) làm vt pháp tuyến, nên có phương trình \(x + 3y - 8 = 0\)
Đường trung trực d của đoạn thẳng AC là đường thẳng đi qua N và nhận vt \(\overrightarrow {AC} = (3; - 1)\) làm vt pháp tuyến, nên có phương trình \(3x - y - 4 = 0\)
\(\Delta \) cắt d tại điểm \(I(2;2)\) cách đều ba điểm A, B, C suy ra đường tròn (C) cần tìm có tâm \(I(2;2)\) và có bán kính \(R = IA = \sqrt 5 \). Vậy (C) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 5\)

Đáp án B
Ta có d 1 đi qua điểm M 1 (7; 3; 9) và có vectơ chỉ phương là u 1 → = (1; 2; 1); d 2 đi qua điểm M 2 (3; 1; 1) và có vectơ chỉ phương là u 2 → .


Cho mặt cầu (S) có bán kính bằng 5. Xét khối tứ diện ABCD có các đỉnh đều thuộc mặt cầu (S) và tam giác ABC vuông cân tại B, DA = DB = DC. Thể tích khối tứ diện ABCD lớn nhất bằng a/b. Với a,b là các số nguyên dương và phân số a/b tối giản. Tính a + b.
A. 1173
B. 4081
C. 128
D. 5035
Cho mặt cầu (S) có bán kính bằng 5. Xét khối tứ diện ABCD có các đỉnh đều thuộc mặt cầu (S) và tam giác ABC vuông cân tại B, DA = DB = DC. Thể tích khối tứ diện ABCD lớn nhất bằng a/b. Với a,b là các số nguyên dương và phân số a/b tối giản. Tính a + b.
A. 1173
B. 4081
C. 128
D. 5035