Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \({d_1}\) song song với đường thẳng \({d_2}:x + 3y + 2 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_2}\) làm vectơ pháp tuyến là \(\overrightarrow n = \left( {1;3} \right)\)
\({d_1}\) đi qua điểm \(A(2;3)\) nên ta có phương trình tổng quát
\(\left( {x - 2} \right) + 3.\left( {y - 3} \right) = 0 \Leftrightarrow x + 3y - 11 = 0\)
b) \({d_1}\) vuông góc với đường thẳng \({d_3}:3x - y + 1 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_3}\) làm vectơ chỉ phương là \(\overrightarrow u = \left( {3; - 1} \right)\)
\({d_1}\) đi qua điểm \(B(4; - 1)\) nên ta có phương trình tham số: \(\left\{ \begin{array}{l}x = 4 + 3t\\y = - 1 - t\end{array} \right.\)

1: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)
2: Vì (d)//y=-3x+2 nên a=-3
Vậy: y=-3x+b
Thay x=3 và y=3 vào y=-3x+b, ta được:
b-9=3
hay b=12

\(y=ax+b\left(d\right);y=-\dfrac{1}{2}x+\dfrac{1}{2}\left(d'\right)\)
\(\left(d\right)\perp\left(d'\right)\Leftrightarrow-\dfrac{1}{2}a=-1\Leftrightarrow a=2\Rightarrow y=2x+b\left(d\right)\)
Lại có \(\left(d\right)\) đi qua \(A\left(-1;2\right)\Rightarrow2=-2+b\Rightarrow b=4\)
\(\Rightarrow y=2x+4\left(d\right)\)

Đường thẳng y = ax + b đi qua hai điểm A(1 ; 3) và B(-1 ; 5) nên:
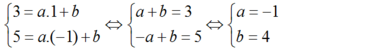
Vậy phương trình đường thẳng là: y = -x + 4.

a) Vì đồ thị hàm số ax+b song song với (d1) nên a=3
hay hàm số có dạng là y=3x+b
Vì đồ thị hàm số y=3x+b đi qua điểm C(3;-2)
nên Thay x=3 và y=-2 vào hàm số y=3x+b, ta được:
\(3\cdot3+b=-2\)
\(\Leftrightarrow b+9=-2\)
hay b=-11
Vậy: Hàm số có dạng là y=3x-11
b) Vì (d)⊥(d2) nên \(a\cdot4=-1\)
hay \(a=-\dfrac{1}{4}\)
Vậy: Hàm số có dạng là \(y=-\dfrac{1}{4}x+b\)
Vì (d) đi qua D(2;-1) nên
Thay x=2 và y=-1 vào hàm số \(y=-\dfrac{1}{4}x+b\), ta được:
\(-\dfrac{1}{4}\cdot2+b=-1\)
\(\Leftrightarrow b-\dfrac{1}{2}=-1\)
hay \(b=-\dfrac{1}{2}\)
Vậy: \(a=-\dfrac{1}{4}\) và \(b=-\dfrac{1}{2}\)

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4a=-28\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-13\end{matrix}\right.\)
b: Vì (d)//y=-2/3x+1 nên a=-2/3
Vậy: (d): y=-2/3x+b
Thay x=4 và y=-3 vào (d), ta được:
b-8/3=-3
hay b=-1/3

a: Vì (d) vuông góc với (Δ) nên -a=-1
hay a=1
Vậy: (d): y=x+b
Thay x=1 và y=-5 vào (d), ta được: b+1=-5
hay b=-6
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}5x^2+4x+3=-3x+3\\y=-3x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(5x+7\right)=0\\y=-3x+3\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(0;3\right);\left(-\dfrac{7}{5};\dfrac{36}{5}\right)\right\}\)

a: Gọi phương trình đường thẳng cần tìm là (d): ax+by+c=0
Vì (d)//3x-2y-5=0 nên (d) có VTPT là (3;-2)
mà (d) đi qua A(0;2)
nên phương trình đường thẳng (d) là:
3(x-0)+(-2)(y-2)=0
=>3x-2y+4=0
b: Gọi phương trình đường thẳng cần tìm là (d): ax+by+c=0
Vì (d)\(\perp\)(3x-2y-5=0) nên (d) nhận \(\overrightarrow{u}=\left(3;-2\right)\) làm vecto chỉ phương
=>VTPT của (d) là (2;3)
mà (d) đi qua A(0;2)
nên phương trình đường thẳng (d) là:
2(x-0)+3(y-2)=0
=>2x+3y-6=0
c: Đặt (d1): \(\left\{{}\begin{matrix}x=1-2t\\y=3-5t\end{matrix}\right.\)
=>VTCP là (-2;-5)=(2;5)
=>VTPT là (-5;2)
Gọi (d): ax+by+c=0 là phương trình đường thẳng cần tìm
Vì (d)//(d1) nên (d) nhận \(\overrightarrow{v}=\left(-5;2\right)\) làm vecto pháp tuyến
Vì (d) nhận \(\overrightarrow{v}=\left(-5;2\right)\) làm vecto pháp tuyến và (d) đi qua B(-1;5) nên phương trình đường thẳng (d) là:
-5(x+1)+2(y-5)=0
=>-5x-5+2y-10=0
=>-5x+2y-15=0
d: Đặt (d2): \(\left\{{}\begin{matrix}x=1-2t\\y=3-5t\end{matrix}\right.\)
=>VTCP là (-2;-5)=(2;5)
Gọi (d): ax+by+c=0 là phương trình đường thẳng cần tìm
Vì (d)\(\perp\)(d2) và \(\overrightarrow{u}=\left(2;5\right)\) là vecto chỉ phương của (d2) nên (d) nhận \(\overrightarrow{u}=\left(2;5\right)\) làm vecto pháp tuyến
mà (d) đi qua B(-1;5)
nên phương trình đường thẳng (d) là:
2(x+1)+5(y-5)=0
=>2x+2+5y-25=0
=>2x+5y-23=0