
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Ta có:\(x^3y^5+3x^3y^5+5x^3y^5+...+\left(2k-1\right)x^3y^5=3249x^3y^5\)
\(x^3y^5\left(1+3+5+...+2k-1\right)=3249x^3y^5\)
\(\Rightarrow1+3+5+...+2k-1=3249\)
\(\Rightarrow\frac{\left(\frac{2k-1-1}{2}+1\right).\left(2k-1+1\right)}{2}=3249\)
\(\Rightarrow\frac{k.2k}{2}=3249\)
\(\Rightarrow k^2=3249\)
\(\Rightarrow k=57\) hoặc k=-57

\(x^3y^5+3x^3y^5+...+\left(2k-1\right)x^3y^5=3249x^3y^5\)
\(\Leftrightarrow x^3y^5\left[1+2+3+...+\left(2k-1\right)\right]=3249x^3y^5\)
\(\Leftrightarrow1+3+5+...+\left(2k-1\right)=3249\)
\(\Leftrightarrow\frac{\left[\left(2k-1\right)+1\right].\left(\frac{\left(2k-1\right)-1}{2}+1\right)}{2}=3249\)
\(\Leftrightarrow\frac{2k.\left(k-1+1\right)}{2}=3249\)
\(\Leftrightarrow\frac{2k^2}{2}=3249\)
\(\Leftrightarrow k^2=3249=57^2\) ( ko xét k = - 57 vì theo quy luật thi k luôn dương )
\(\Rightarrow k=57\)

Nhìn biểu thức có vẻ rối, nhưng ta chẳng cần quan tâm cái biến làm gì cả.
Coi như không có biến, ta có :
\(1+3+5+...+\left(2k-1\right)=3249\)
\(\Rightarrow\dfrac{\dfrac{\left(2k-1\right)-1}{2}+1}{2}\cdot\left(2x-1+1\right)=3249\)
\(\Rightarrow CALC\left(k\right)=57\)
Vậy \(k=57\)

a: \(3x^2\left(2x^3-x+5\right)\)
\(=3x^2\cdot2x^3-3x^2\cdot x+5\cdot3x^2\)
\(=6x^5-3x^3+15x^2\)
b: \(x^2y\left(4xy+3y-5x\right)\)
\(=x^2y\cdot4xy+x^2y\cdot3y-x^2y\cdot5x\)
\(=4x^3y^2+3x^2y^2-5x^3y\)
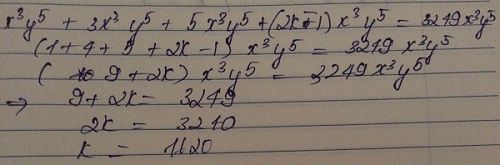
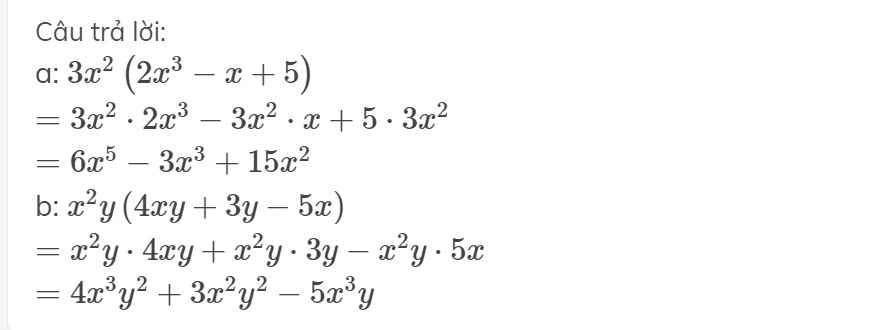
k là cái j , bài ko có k