|x+2|+|x+3/5|+|x+1/2|=4x

Khách

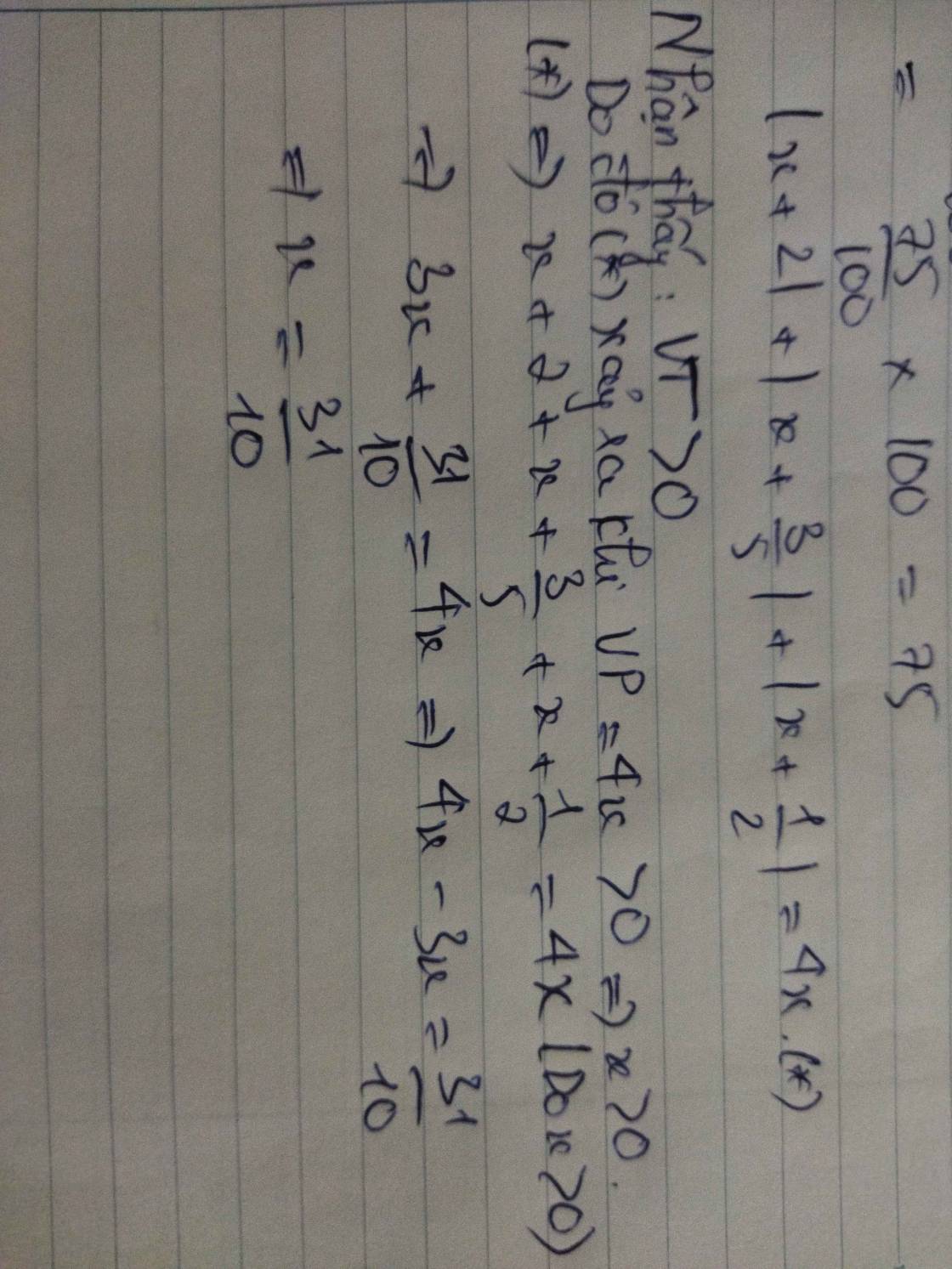
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Dương Đỗ đai

29 tháng 12 2023 - olm

|x+2|+|x+3/5|+|x+1/2|=4x

#Hỏi cộng đồng OLM #Toán lớp 7

Dang Tung

CTVHS

29 tháng 12 2023

Đúng(1)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Nguyễn Đỗ Huy

3 tháng 6 2016 - olm

tìm x biết:

a)(2x+2)(2x-2)-4x(x+5)=8

b)(4x+5)(4x-5)-8x(2x-7)=11

c)(1/2x-3)(1/2x+3)-1/4x(x+5)=11/2

d)(3x+2)(3x-2)-4x(x+2-5x²=18

#Hỏi cộng đồng OLM #Toán lớp 7

VRCT_Vy Larkyra

3 tháng 6 2016

\(a.x=-0,6\)

\(c.x=-11,6\)

Pt nhju ak!!!

Đúng(0)

Nguyễn Thị Lan Anh

8 tháng 2 2017

tìm x biết

1) |x+1|+|x-2|+|x+3|=6

2) |1-x|+3|x-3|-2|x-2|=x

3) |x+1|+|x+2|+|x+3|=4x

4) |x+1|+|x+2|+|x+3|+|x+4|=5x+1

5)||2x-3|-x+1|=4x-1

#Hỏi cộng đồng OLM #Toán lớp 7

Nguyen Phuong Vy

18 tháng 10 2016 - olm

Tìm GTNN,GTLN

a) A= (x-1) (x-3) + 11

b) B= 5 - 4x² + 4x

c) C= (x²-3x+1) (x²-3x-1)

d) D= (x-1) (x+5) (x²+4x+5)

#Hỏi cộng đồng OLM #Toán lớp 7

Tiên Lê

20 tháng 6 2017

Tìm Min

x^2 +4x-5

4x^2+4x-3

x^2+x+1

2x^2+4x+8

x^2+x

#Hỏi cộng đồng OLM #Toán lớp 7

Đức Hiếu

20 tháng 6 2017

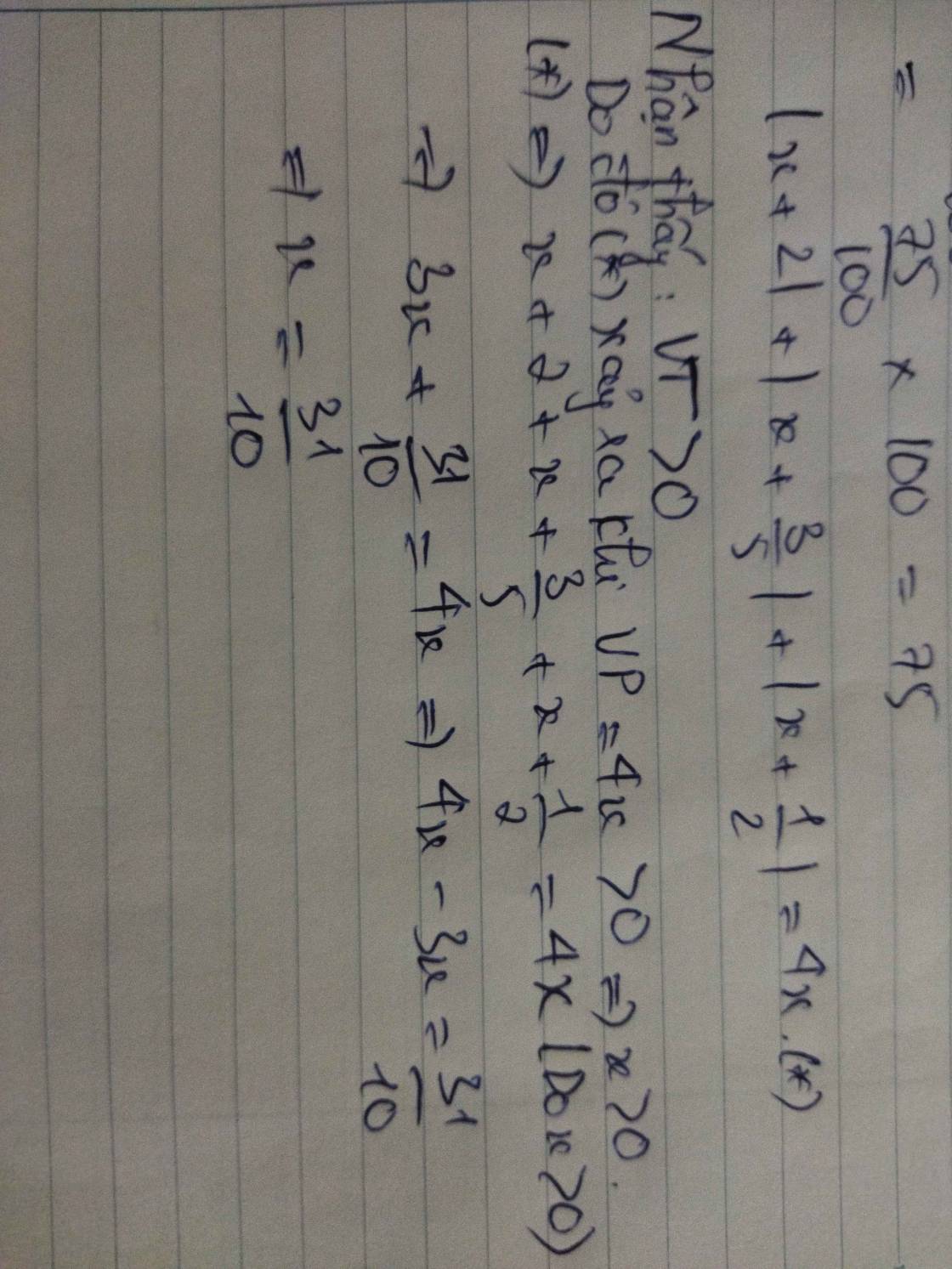
a, \(x^2+4x-5=x^2+2x+2x+4-9\)

\(=\left(x^2+2x\right)+\left(2x+4\right)-9\)

\(=x.\left(x+2\right)+2.\left(x+2\right)-9\)

\(=\left(x+2\right)^2-9\)

Với mọi giá trị của \(x\in R\) ta có:

\(\left(x+2\right)^2\ge0\Rightarrow\left(x+2\right)^2-9\ge-9\) với mọi giá trị của \(x\in R\).

Để \(\left(x+2\right)^2-9=-9\) thì \(\left(x+2\right)^2=0\Rightarrow x=-2\)

Vậy.......

b, \(4x^2+4x-3=4x^2+2x+2x+1-4\)

\(=2x.\left(2x+1\right)+\left(2x+1\right)-4\)

\(=\left(2x+1\right)^2-4\)

Với mọi giá trị của \(x\in R\) ta có:

\(\left(2x+1\right)^2\ge0\Rightarrow\left(2x+1\right)^2-4\ge-4\) với mọi giá trị của \(x\in R\).

Để \(\left(2x+1\right)^2-4=-4\) thì \(\left(2x+1\right)^2=0\Rightarrow x=\dfrac{-1}{2}\)

Vậy.........

c, \(x^2+x+1=x^2+\dfrac{1}{2}x+\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=x.\left(x+\dfrac{1}{2}\right)+\dfrac{1}{2}.\left(x+\dfrac{1}{2}\right)+\dfrac{3}{4}\)

\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)

Với mọi giá trị của \(x\in R\) ta có:

\(\left(x+\dfrac{1}{2}\right)^2\ge0\Rightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\) với mọi giá trị của \(x\in R\).

Để \(\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\) thì \(\left(x+\dfrac{1}{2}\right)^2=0\Rightarrow x=\dfrac{-1}{2}\)

Vậy.........

Chúc bạn học tốt!!!

Các câu còn lại làm tương tự!!

Đúng(0)

Hà Linh

20 tháng 6 2017

a) A = x² + 4x - 5

A = x² + 4x + 4 +1 = ( x + 2 )² + 1 \(\ge\) 1 với mọi x

Min_A = 1 khi và chỉ khi x = -2

b) B = 4x² + 4x - 3

B = 4x² + 4x + 1 - 4

B = ( 2x+1 )² - 4 \(\ge\) -4 với mọi x

Min_B = -4 khi và chỉ khi x = \(\dfrac{-1}{2}\)

c) C = x²+ x + 1

C = x² + x + \(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)

C = ( x + \(\dfrac{1}{2}\) )²+ \(\dfrac{3}{4}\) \(\ge\) \(\dfrac{3}{4}\) với mọi x

Min_C = \(\dfrac{3}{4}\) khi và chỉ khi x = \(-\dfrac{1}{2}\)

d) D = 2x² + 4x + 8

D = 2 . ( x²+ 2x + 4 )

D = 2. ( x² + 2x + 1 + 3 )

D = 2. \(\left[\left(x+1\right)^2+3\right]\)

D = 2.( x+1 )² + 6 \(\ge\) 6 với mọi x

Min_D = 6 khi và chỉ khi x = -1

e) E = x² + x

E = x² + x + \(\dfrac{1}{4}\) - \(\dfrac{1}{4}\)

E = \(\left(x+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\) \(\ge\) \(-\dfrac{1}{4}\) với mọi x

Min_E= \(-\dfrac{1}{4}\) khi và chỉ khi x = \(\dfrac{-1}{2}\)

Đúng(0)

kiet hà

30 tháng 4 2023

tìm x

5)
4x x 5 x 4x 3 5
6)
2
2
x 2 x 1 6
7)
2
3
(3 2) 3 .
4
x x x   
8) (3x + 1). (2x- 3) – 6x.(x + 2) = 16

#Hỏi cộng đồng OLM #Toán lớp 7

Nguyễn Lê Phước Thịnh

30 tháng 4 2023

8: =>6x^2-9x+2x-3-6x^2-12x=16

=>-19x=19

=>x=-1

Đúng(1)

Nguyen Thang

7 tháng 10 2016 - olm

Tìm x biết
a) (7^x-2+7^x-1+7)/57=(5^x+5^2x+1+5^2x+3)/131
b) (4x-3)^4=(4x-3)^2

#Hỏi cộng đồng OLM #Toán lớp 7

Mây Phiêu Du

14 tháng 8 2015 - olm

Cho 2 đa thức : P(x) = x^5 - 2x^2 + 7x^4 - 9x^3 - 1/4x ; Q(x) = 5x^4 - x^5 + 4x^2 - 2x^3 - 1/4

Tính : P(x) + Q(x) và P(x) - Q(x)

#Hỏi cộng đồng OLM #Toán lớp 7

Bùi Anh Khoa

31 tháng 10 2018 - olm

Tìm x:

|5x-3|-3x=7

|x-3|+|x-5|-4x=-28

\(\left|x+2\right|+\left|x+\frac{3}{5}\right|+\left|x+\frac{1}{2}\right|=4x\)

\(\left|2x-1\right|+\left(4x^2-1\right)^2=0\)

#Hỏi cộng đồng OLM #Toán lớp 7

Incursion_03

31 tháng 10 2018

|5x-3| - 3x = 7

*Nếu \(x\ge\frac{3}{5}\)

5x - 3 - 3x = 7

2x = 10

x = 5 ( tm)

*Nếu \(x< \frac{3}{5}\)

3 - 5x - 3x = 7

-8x = 4

x = \(-\frac{1}{2}\)( tm )

Làm hơi khó nhìn , thông cảm. Mệt rùi :)

Đúng(0)

Incursion_03

31 tháng 10 2018

|x - 3| + |x - 5| - 4x = -28

*Nếu x < 3

3 - x + 5 - x - 4x = -28

-6x = -36

x = 6 ( loại do ko tm khoảng đang xét )

* nếu 3 < x < 5

x - 3 + 5 - x - 4x = -28

-4x = -30

x= \(\frac{15}{2}\) ( loại do ko tm khaongr đang xét )

*Nếu x > 5

x - 3 + x - 5 - 4x = -28

-2x = -20

x = 10 ( tm)

Vậy x =10

Đúng(0)

hải trung

12 tháng 3 2022

Tìm x biết a) (x^2-4x+5)_(x^2-2x+1)=3 lớp 7

b)(4x^3-5X^2+3x-1)+(3-5x+5x^2-4x^3)=2

c)(3x-2)-(5x+4)=(x-3)-(X+5)

#Hỏi cộng đồng OLM #Toán lớp 7

Nguyễn Huy Tú

12 tháng 3 2022

a, \(-4x+5+2x-1=3\Leftrightarrow-2x=-1\Leftrightarrow x=\dfrac{1}{2}\)

b, \(-2x+2=2\Leftrightarrow x=0\)

c, \(-2x-6=-8\Leftrightarrow x=1\)

Đúng(1)

nguyễn thị nga

6 tháng 5 2019 - olm

f(x)=-3x(x-2)+5x^4-x^2(x-3)-6x+2

g(x)=2x^2(x^2+3)-4x^3-4x^3+2(x-1)+5

Tinh h(x)=f(x)+g(x) roi tinh h(-1)

Tinh q(x)=f(x)-g(x) roi tinh q(-2)

#Hỏi cộng đồng OLM #Toán lớp 7

Đỗ Thị Dung

6 tháng 5 2019

h(x) = f(x) + g(x) =\(-3x\left(x-2\right)+5x^4-x^2\left(x-3\right)-6x+2\)2 + \(2x^2\left(x^2+3\right)-4x^3-4x^3+2\left(x-1\right)+5\)

= \(-3x^2+6x+5x^4-x^3+3x^2-6x+2+2x^4+6x^2\)-\(4x^3-4x^3+2x-2+5\)

mk làm ra đến đây rồi, bạn tự làm tp nhé, phần sau dễ thôi

sau đó thay h(-1) vào rồi tính nhé

câu sau làm tương tự

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP