TC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 5 2017
a) (5x2y-5xy2+xy) + (xy-x2y2+5xy2)
= 5x2y-5xy2+xy+xy-x2y2+5xy2
= 5x2y+(5xy2-5xy2)+(xy+xy)-x2y2
= 5x2y+2xy-x2y2
b) (x2+y2+z2) + (x2-y2+z2)
= x2+y2+z2+x2-y2+z2
= (x2+x2)+(y2-y2)+(z2+z2)
= 2x2+2z2
LM
11 tháng 1 2018
a)( \(5x^2y\)\(-\) \(5xy^2\) \(+\) \(xy\)) + (\(xy\) \(-\) \(x^2y^2\) \(+\) \(5xy^2\))
= \(5x^2y-5xy^2+xy+xy-x^2y^2+5xy^2\)
= \(5x^2y+2xy-x^2y^2\)
b) \(\left(x^2+y^2+z^2\right)+\left(x^2-y^2+z^2\right)\)
= \(x^2+y^2+z^2+x^2-y^2+z^2\)
=\(2x^2+2z^2\)
=\(2\left(x+z\right)^2\)
19 tháng 7 2018
Ta có :
\(Q+P\)
\(=3xyz+2.5xy^2-2+2xyz+1.5xyz-y^3\)
\(=6.5xyz+2.5xy^2-y^3-2\)
\(Q-P=3xyz+2.5xy^2-2-2xyz-1.5xyz+y^3\)
\(=2.5xy^2-0.5xyz+y^3-2\)
\(P-Q=2xyz+1.5xyz-y^3-3xyz-2.5xy^2+2\)
\(=0.5xyz-y^3-2.5xy^2+2\)
25 tháng 6 2019
a) Thiếu đề
b) Áp dụng t/c của dãy tỉ số bằng nhau, ta có :
\(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) => \(\frac{4x}{4}=\frac{3y}{6}=\frac{2z}{6}=\frac{4x+3y+2z}{4+6+6}=\frac{14}{16}=\frac{7}{8}\)
=> \(\hept{\begin{cases}\frac{x}{1}=\frac{7}{8}\\\frac{y}{2}=\frac{7}{8}\\\frac{z}{3}=\frac{7}{8}\end{cases}}\) => \(\hept{\begin{cases}x=\frac{7}{8}.1=\frac{7}{8}\\y=\frac{7}{8}.2=\frac{7}{4}\\z=\frac{7}{8}.3=\frac{21}{8}\end{cases}}\)
Vậy ...
25 tháng 6 2019
Sửa lại xíu :
\(a)\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)và \(x-2y+3z=14\)
\(b)\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\)và \(4x+3y+2z=36\)
1 tháng 4 2018
thay x= -1/2 ; y= 4; z =6 vào biểu thức A
có: \(A=\left(\frac{-1}{2}\right)^2.4+\left(\left(\frac{-1}{2}\right)^3-3.\frac{-1}{2}.4.6\right)+\left(-14^{15}\right)^0\)
\(A=\frac{1}{4}.4+\left(\frac{-1}{8}-\left(-36\right)\right)+1\)
\(A=1+35\frac{7}{8}+1\)
\(A=37\frac{7}{8}\)
KL: \(A=37\frac{7}{8}\) tại x= -1/2 ; y=4; z=6
CHÚC BN HỌC TỐT!!!
22 tháng 7 2019
Câu 1: ĐẶt \(\frac{x}{5}=\frac{y}{4}=k\)\(\Rightarrow x=5k;......y=4k\)
Ta có: \(x^2y=\left(5k\right)^2.\left(4k\right)=400k^3=100\)
\(\Rightarrow k^3=\frac{1}{4}\Rightarrow k=\sqrt[3]{\frac{1}{4}}\)
Vậy \(x=5k=4\sqrt[3]{\frac{1}{4}}\)
\(y=4.\sqrt[3]{\frac{1}{4}}\)
Câu 3 4 5 tương tư:
câu 2. bạn biến đổi: \(5x=2y\Leftrightarrow\frac{x}{2}=\frac{y}{5}\)thì sẽ trở thành dạng quen thuộc ở trên. :))
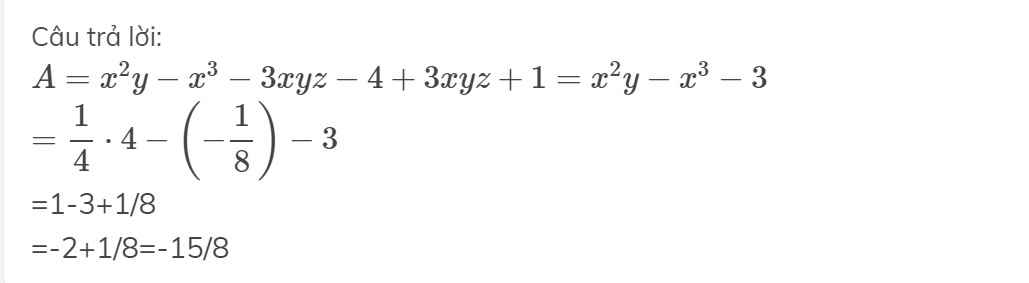
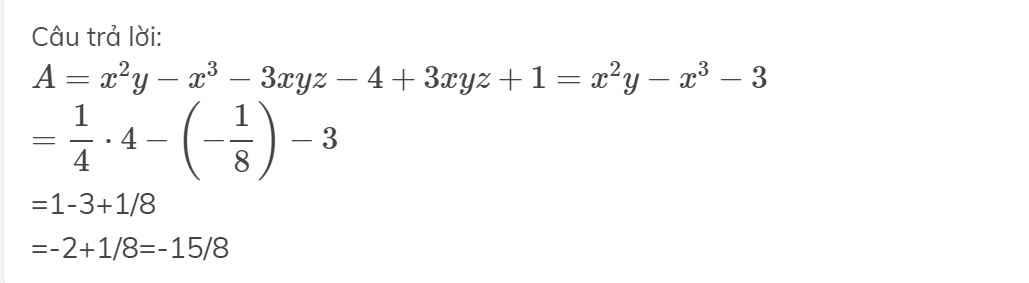
P = x^2 - 2xyz + z^2
Q = 5x^2 + 3xyz - z^2
=> P + Q = 6x^2 + xyz
P - Q = -4x^2 - 5xyz + 2z^2
\(P+Q=x^2-2xyz-z^2+3xyz-z^2+5x^2\)
\(=\left(x^2+5x^2\right)+\left(-2xyz+3xyz\right)+\left(-z^2-z^2\right)\)
\(=6x^2+xyz-2z^2\)
\(P-Q=x^2-2xyz-z^2-3xyz+z^2-5x^2\)
\(=\left(x^2-5x^2\right)+\left(-2xyz-3xyz\right)+\left(-z^2+z^2\right)\)
\(=-4x^2-5xyz\)