Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Ta có 
và 
,
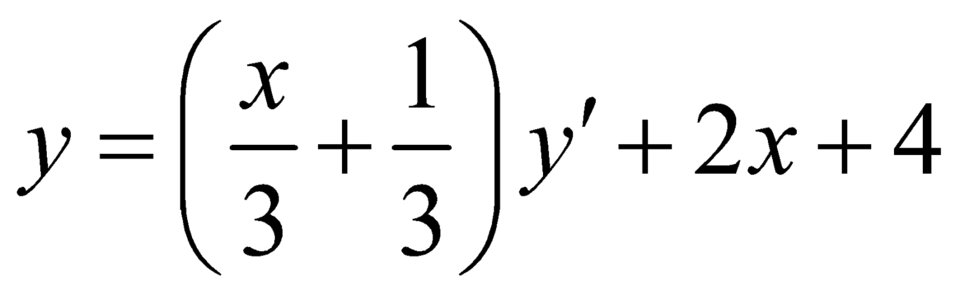Duy ra phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là 
, 
.
Đường tròn 
có tâm 
và bán kính 
.
Đường thẳng 
tiếp xúc với đường tròn 
khi và chỉ khi 
.
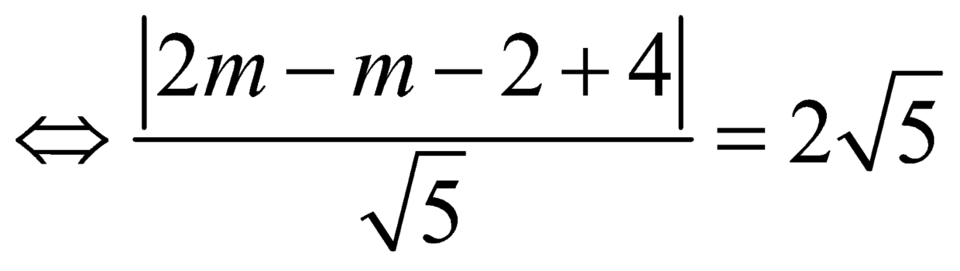
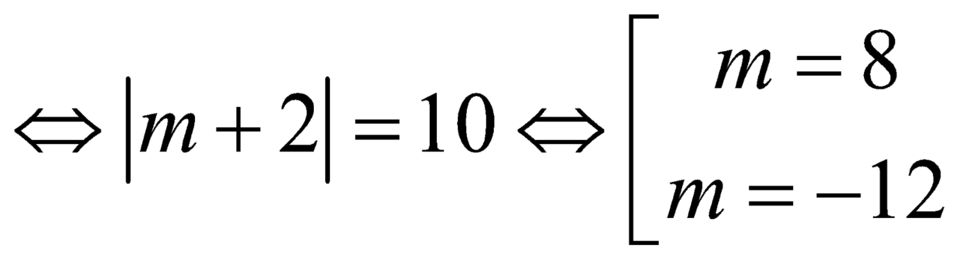Vậy 
.
a.
\(y'=\frac{-1-m^2}{\left(x-1\right)^2}< 0\Rightarrow\) hàm nghịch biến trên mỗi khoảng xác định
\(\Rightarrow\) Không tồn tại GTLN của hàm trên \(\left[1;3\right]\) (chắc bạn ghi sai đề bài vì trên [1;3] có điểm đặc biệt \(x=1\) khiến hàm ko xác định đồng thời hàm nghịch biến nên \(y_{max}=+\infty\) trên đoạn này)
b.
\(y\ge3\) ; \(\forall x\in\left[-3;0\right]\Leftrightarrow\min\limits_{\left[-3;0\right]}y\ge3\)
Xét hàm \(f\left(x\right)=x^4-2x^2+1-m\)
\(f'\left(x\right)=4x^3-4x=0\Rightarrow x=\left\{-1;0;1\right\}\)
\(f\left(-3\right)=64-m\) ; \(f\left(-1\right)=m\) ; \(f\left(0\right)=1-m\)
Nếu \(f\left(x\right)=0\) có nghiệm thuộc \(\left[-3;0\right]\Leftrightarrow0\le m\le64\) thì \(\min\limits_{\left[-3;0\right]}y=0\) (ktm)
\(\Rightarrow\left[{}\begin{matrix}m< 0\\m>64\end{matrix}\right.\)
Khi đó \(\min\limits_{\left[-3;0\right]}=min\left\{\left|64-m\right|;\left|m\right|\right\}\)
- Nếu \(y_{min}=\left|64-m\right|\Rightarrow\left\{{}\begin{matrix}\left|m\right|\ge\left|64-m\right|\\\left|64-m\right|\ge3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ge32\\\left[{}\begin{matrix}m\ge67\\m\le61\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m\ge67\)
- Nếu \(y_{min}=\left|m\right|\Rightarrow\left\{{}\begin{matrix}\left|64-m\right|\ge\left|m\right|\\\left|m\right|\ge3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le32\\\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m\le-3\)
Vậy \(\left[{}\begin{matrix}m\ge67\\m\le-3\end{matrix}\right.\)
Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.
bn ơi câu a t chưa làm chưa biết nhưng câu b chắc chắn có Max tại x=-3 nhé ! Nếu bn chỉ tìm ra Min là chưa đủ
1. Không rõ đề
2.
\(y'=\sqrt{x^2+3}+\frac{x\left(x-6\right)}{\sqrt{x^2+3}}=\frac{2x^2-6x+3}{\sqrt{x^2+3}}< 0;\forall x\in\left[1;2\right]\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left[1;2\right]\Rightarrow y_{max}=y\left(1\right)=-10\)
3.
\(y'=3x^2-4mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\frac{4m}{3}\end{matrix}\right.\)
Ta có: \(y\left(1\right)=3-3m\) ; \(y\left(3\right)=29-19m\)
TH1: \(\frac{4m}{3}\le1\Rightarrow m\le\frac{3}{4}\) khi đó hàm đồng biến trên \(\left[1;3\right]\Rightarrow y_{max}=y\left(3\right)\)
\(\Rightarrow29-19m=6\Leftrightarrow m=\frac{23}{19}>\frac{3}{4}\left(ktm\right)\)
TH2: \(\frac{4m}{3}\ge3\Rightarrow m\ge\frac{9}{4}\)
Khi đó hàm nghịch biến trên \(\left[1;3\right]\Rightarrow y_{max}=y\left(1\right)\)
\(\Rightarrow3-3m=6\Rightarrow m=-1< \frac{9}{4}\left(ktm\right)\)
TH3: \(1< \frac{4m}{3}< 3\Rightarrow\frac{3}{4}< m< \frac{9}{4}\)
Hàm nghịch biến trên \(\left(1;\frac{4m}{3}\right)\) và đồng biến trên \(\left(\frac{4m}{3};3\right)\)
\(\Rightarrow\) Hàm đạt GTLN tại \(x=1\) hoặc \(x=3\)
\(y\left(1\right)=3-3m=6\Rightarrow m=-1\notin\left(\frac{3}{4};\frac{9}{4}\right)\) (loại)
\(y\left(3\right)=29-19m=6\Rightarrow m=\frac{23}{19}\in\left(\frac{3}{4};\frac{9}{4}\right)\)
Vậy \(m=\frac{23}{19}\)