Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

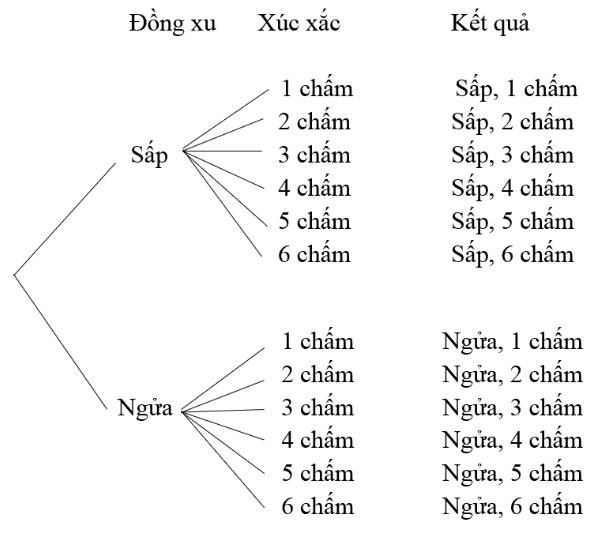
a) Kết quả của đồng xu và xúc xắc xảy ra đồng thời nên kết quả xảy ra gồm 2 kết quả liên tiếp nhau
Kết quả 1: Kết quả của đồng xu, có 2 kết quả: Sấp và ngửa
Kết quả 2: Kết quả của xúc xắc, có 6 kết quả: mỗi kết quả của mỗi mặt con xúc xắc
Áp dụng quy tắc nhân, ta có số kết quả có thẻ xuất hiện khi gieo đồng thời một đồng xu và một con xúc xắc là:
\(2.6 = 12\)
Vậy có 12 kết quả có thể xáy ra
b)

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

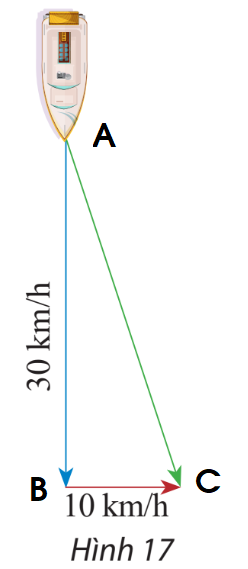
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

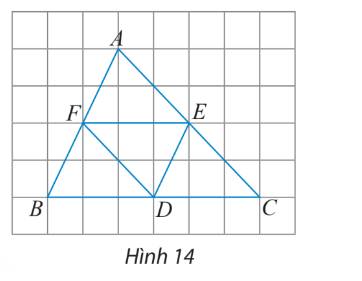
Từ giả thiết ta có:
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

Trong toán học, mỗi cách xếp thứ tự đá luân lưu của 5 cầu thủ được gọi là hoán vị.

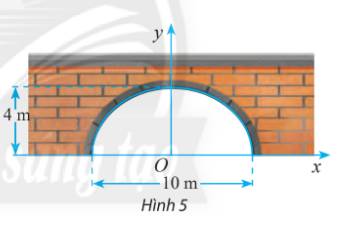
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

a) Số trung bình điểm thi Ngữ văn của lớp 10C và 10D tương ứng là
.(3x5 + 7x6 + 12x7 + 14x8 + 3x9 + 1x10) = 7,25
.(8x6+18x7+10x8+4x9) = 7,25.
Phương sai bảng điểm thi Văn của hai lớp theo thứ tự là:
= 1,2875
= 0,7875.
Độ lệch chuẩn theo thứ tự là Sx ≈ 1,1347 Sy ≈ 0,8874.
b) Qua xem xét các số đặc trung ta thấy điểm trung bình thi văn 2 lớp 10C và 10D là như nhau (đều bằng 7,25). Nhưng phương sai của bảng điểm thi lớp 10D nhỏ hơn phương sai tương ứng ở lớp 10C. Điều đó chứng tỏ kết quả làm bài thi Văn ở lớp 10D đồng đều hơn.
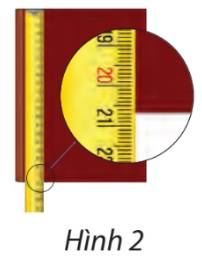






Quan sát Hình 2, ta thấy: Chiều dài trang bìa sổ gần tới vạch thứ 7 giữa số 20 và 21.
Do đó quyển sổ dài gần 20,7 cm.
Vậy kết quả của bạn Hoa có sai số nhỏ hơn.