Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Viết phương trình tham số của đường thẳng d trong các trường hợp sau:
a) d đi qua điểm M(5 ; 4 ; 1) có vec tơ chỉ phương
#Hỏi cộng đồng OLM
#Mẫu giáo
a) Phương trình đường thẳng d có dạng: , với t ∈ R.
b) Đường thẳng d vuông góc với mặt phẳng (α): x + y - z + 5 = 0 nên có vectơ chỉ phương
(1 ; 1 ; -1) vì
là vectơ pháp tuyến của (α).
Do vậy phương trình tham số của d có dạng:
c) Vectơ (2 ; 3 ; 4) là vectơ chỉ phương của ∆. Vì d // ∆ nên
cùng là vectơ chỉ phương của d. Phương trình tham số của d có dạng:
d) Đường thẳng d đi qua hai điểm P(1 ; 2 ; 3) và Q(5 ; 4 ; 4) có vectơ chỉ phương
(4 ; 2 ; -1) nên phương trình tham số có dạng:
HD: Ta có
Cả 4 đáp án đều thỏa mãn về VTCP, ta xét điểm đi qua.
Thay tọa độ (-5;-10;-15),(2;4;6),(1;2;3),(3;6;12) vào phương trình
thì ta thấy (3;6;12) không thỏa mãn. Chọn D.
Đường thẳng đi qua điểm M x 0 ; y 0 ; z 0 và VTCP u ⇀ = a ; b ; c có phương trình là
x = x 0 + a t y = y 0 + b t c = c 0 + c t
Đường thẳng ∆ đi qua điểm M(2;0;-1) và có một véc tơ chỉ phương a ⇀ = 4 ; - 6 ; 2
hay 1 2 a ⇀ = 2 ; - 3 ; 1
nên ∆ : x = 2 + 2 t y = - 3 t z = - 1 + t
Chọn đáp án B.
Phương trình đường thẳng d là d: x = 1 + 2 t y = - 2 + 3 t z = 4 - 5 t
Chọn đáp án A.
Đáp án D.
Phương trình tham số của D là
x = 2 + 2 t y = − 3 t z = − 1 + t
Đáp án B
Phương pháp:
Điều kiện để hai đường thẳng trùng nhau là hai véc tơ chỉ phương cùng phương và một điểm thuộc đường thẳng này cũng thuộc đường thẳng kia
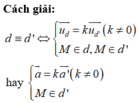
a) Phương trình đường thẳng d có dạng: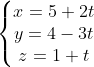
, với t ∈ R.
b) Đường thẳng d vuông góc với mặt phẳng (α): x + y - z + 5 = 0 nên có vectơ chỉ phương
Do vậy phương trình tham số của d có dạng:
c) Vectơ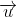
(2 ; 3 ; 4) là vectơ chỉ phương của ∆. Vì d // ∆ nên 
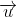cùng là vectơ chỉ phương của d. Phương trình tham số của d có dạng:
d) Đường thẳng d đi qua hai điểm P(1 ; 2 ; 3) và Q(5 ; 4 ; 4) có vectơ chỉ phương