Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có phương trình 3x - y = 2 (1)
Vì (1) \(\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=3x-2\end{matrix}\right.\)
+ Vẽ đưởng thẳng biểu diễn tập nghiệm của phương trình:
Với y = 3x - 2
Cho x = 0 => y = -2 được A(0; 2).
Cho y = 0 => 3x = 2 => x = ta được B(
; 0).
Biều diễn cặp số A(0; 2) và B(; 0) trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình 3x - y = 2.
b) x + 5y = 3 \(\Leftrightarrow\left\{{}\begin{matrix}x=-5y+3\\y\in R\end{matrix}\right.\)
Ta được nghiệm tổng quát của phương trình là (-5y + 3, y)
Hay \(\left\{{}\begin{matrix}x=-5y+3\\y\in R\end{matrix}\right.\)
Biểu diễn hình học: tập nghiệm là đường thẳng AB với A(3; 0) B(-2; 1).
\(4x-3y=-1\Leftrightarrow\left\{{}\begin{matrix}x\in R\\3y=4x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=\dfrac{4}{3}x+\dfrac{1}{3}\end{matrix}\right.\)
Tập nghiệm là đường thẳng qua A (0; \(\dfrac{1}{3}\)) và B (\(\dfrac{-1}{4}\); 0)

d) \(x+5y=0\Leftrightarrow\left\{{}\begin{matrix}x=-5y\\y\in R\end{matrix}\right.\)
Tập nghiệm là đường thẳng qua O(0; 0) và A(-5; 1).
e) \(4x+0y=-2\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-1}{2}\\y\in R\end{matrix}\right.\)
Tập nghiệm là đường thẳng x = \(\dfrac{-1}{2}\), qua A(\(\dfrac{-1}{2}\); 0) và song song với trục tung.
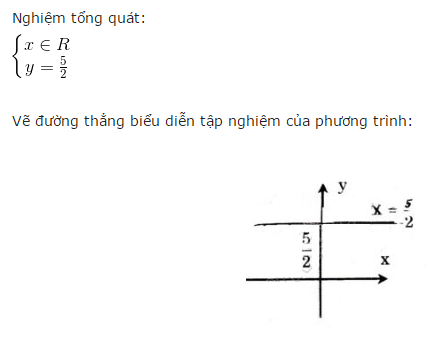
f) \(0x+2y=5\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=\dfrac{5}{2}\end{matrix}\right.\)
a) Ta có phương trình 3x - y = 2 (1)
Vì (1) ⇔{x∈Ry=3x−2⇔{x∈Ry=3x−2
+ Vẽ đưởng thẳng biểu diễn tập nghiệm của phương trình:
Với y = 3x - 2
Cho x = 0 => y = -2 được A(0; 2).
Cho y = 0 => 3x = 2 => x = ta được B(
; 0).
Biều diễn cặp số A(0; 2) và B(; 0) trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình 3x - y = 2.
b) x + 5y = 3 ⇔{x=−5y+3y∈R⇔{x=−5y+3y∈R
Ta được nghiệm tổng quát của phương trình là (-5y + 3, y)
Hay {x=−5y+3y∈R{x=−5y+3y∈R
Biểu diễn hình học: tập nghiệm là đường thẳng AB với A(3; 0) B(-2; 1).
4x−3y=−1⇔{x∈R3y=4x+14x−3y=−1⇔{x∈R3y=4x+1
⇔⎧⎨⎩x∈Ry=43x+13⇔{x∈Ry=43x+13
Tập nghiệm là đường thẳng qua A (0; 1313) và B (

\(a,\)\(\hept{\begin{cases}3x+y=3\\2x-y=7\end{cases}}\)\(\Rightarrow3x+y+2x-y=3+7\)\(\Rightarrow5x=10\Rightarrow x=2\)
Mà \(3x+y=3\Rightarrow3.2+y=3\Rightarrow y=3-6=-3\)
Vậy \(\hept{\begin{cases}x=2\\y=-3\end{cases}}\)
\(b,\hept{\begin{cases}2x+5y=8\\2x-3y=0\end{cases}}\)\(\Rightarrow2x+5y-\left(2x-3y\right)=8-0\)
\(\Rightarrow2x+5y-2x+3y=8\)\(\Rightarrow8y=8\Rightarrow y=1\)
Mà \(2x+5y=8\Rightarrow2x+5=8\Rightarrow2x=\frac{8-5}{2}=\frac{3}{2}\)
Vậy \(\hept{\begin{cases}x=\frac{3}{2}\\y=1\end{cases}}\)
\(c,\hept{\begin{cases}4x+3y=6\\2x+y=4\end{cases}\Rightarrow\hept{\begin{cases}4x+3y=6\\4x+2y=8\end{cases}}}\)
\(\Rightarrow4x+3y-\left(4x+2y\right)=6-8\)
\(\Rightarrow4x+3y-4x-2y=-2\)
\(\Rightarrow y=-2\)
Mà \(4x+3y=6\Rightarrow4x-6=6\Rightarrow4x=12\Leftrightarrow x=3\)
Vậy \(\hept{\begin{cases}x=3\\y=-2\end{cases}}\)
Làm tương tự nha cậu

a)\(\left\{{}\begin{matrix}8x+2y=4\\8x+3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\4x+1=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}y=1\\x=\frac{1}{4}\end{matrix}\right.\)b)
\(\left\{{}\begin{matrix}12x-8y=44\\12x-15y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=35\\4x-5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\4x-5.5=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=7\end{matrix}\right.\)c)\(\left\{{}\begin{matrix}9x=-18\\4x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\4.\left(-2\right)+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=7\end{matrix}\right.\)


 Còn lại tương tự
Còn lại tương tự
a: 2x-y=3
nên y=2x-3
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=2x-3\end{matrix}\right.\)
b: x+2y=4
nên x=4-2y
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=4-2y\end{matrix}\right.\)
c: 3x-2y=6
nên 3x=2y+6
hay \(x=\dfrac{1}{2}y+2\)
Vậy: Nghiệm là \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{1}{2}y+2\end{matrix}\right.\)
d: 2x+3y=5
nên 2x=5-3y
hay x=-3/2y+5/2
Vậy: \(\left\{{}\begin{matrix}y\in R\\x=-\dfrac{3}{2}y+\dfrac{5}{2}\end{matrix}\right.\)