Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

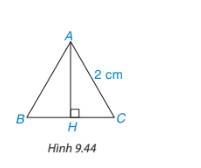
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1,73cm.

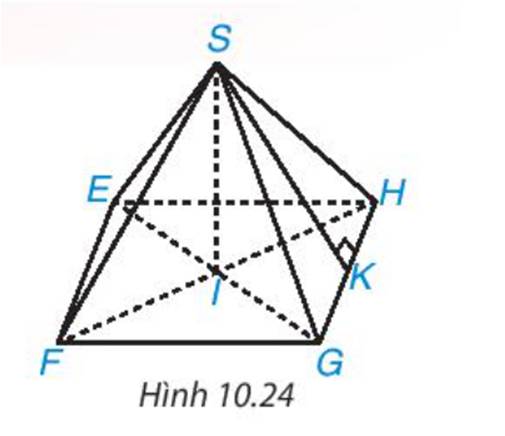
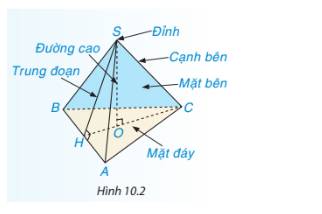
- Đỉnh: S
- Cạnh bên: SE, SF, SG, SH
- Mặt bên: SEF, SFG, SGH. SEH
- Mặt đáy: EFGH
- Đường cao: SI
- Một trung đoạn: SK

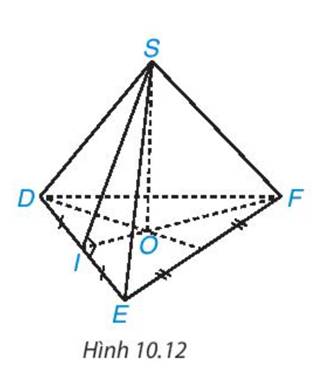
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: SDE, SEF, SDF
- Mặt đáy: DEF
- Đường cao: SO
- Một trung đoạn: SI

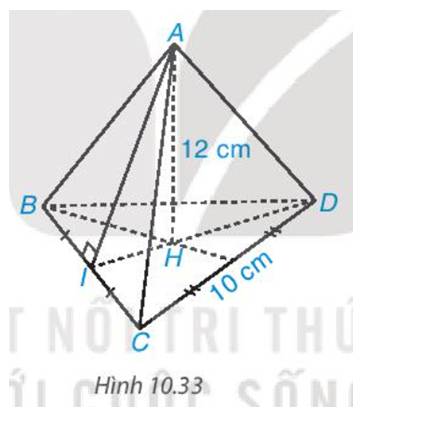
- Xét tam giác BID vuông tại I, có
\(I{{\rm{D}}^2} = B{{\rm{D}}^2} - B{I^2} = {10^2} - {5^2}\)
=> ID ≈ 8,66 (cm)
- Diện tích tam giác BCD là:
\({S_{BC{\rm{D}}}} = \frac{1}{2}.I{\rm{D}}.BC = \frac{1}{2}.8,66.10 = 43,3\left( {c{m^2}} \right)\)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.43,3.12 \approx 173,2(c{m^3})\)

Hình chóp tam giác đều S. ABC có:
- Đỉnh: S
- Cạnh bên: SA, SB, SC.
- Mặt đáy: tam giác ABC.
- Đường cao: SO.
- Trung đoạn: SH
Một khối gỗ gồm đế là hình lập phương cạnh 9 cm và một hình chóp tứ giác đều. Tính thể tích khối gỗ.
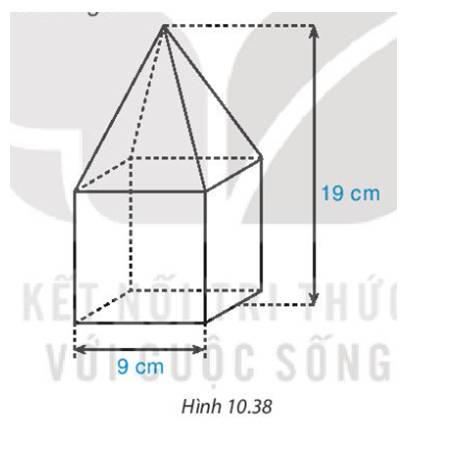

Có chiều cao của cả khối gỗ là 9 cm, chiều cao cụa hình lập phương là 9 cm
=> Chiều cao của hình chóp tứ giác đều là: 19−9=10 (cm)
- Diện tích mặt đáy của hình chóp tứ giác đều là: 9.9=81 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.81.10 = 270\left( {c{m^3}} \right)\)
- Thể tích hình lập phương là: V=9.9.9=729 \(\left( {c{m^3}} \right)\)
Vậy thể tích của khối gỗ là: 270+729= 999 (cm3)

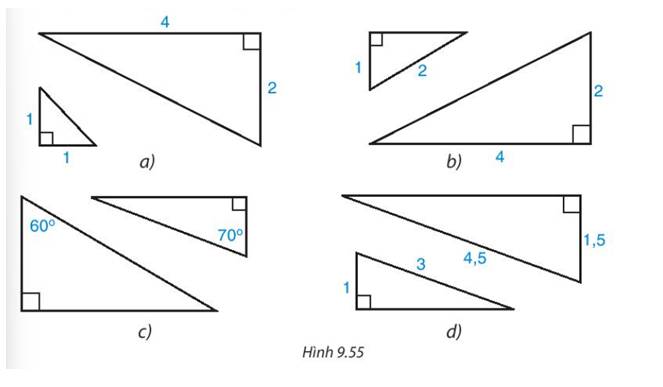
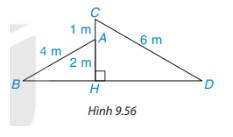
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

Xét hai tam giác vuông HBA và tam giác vuông HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)

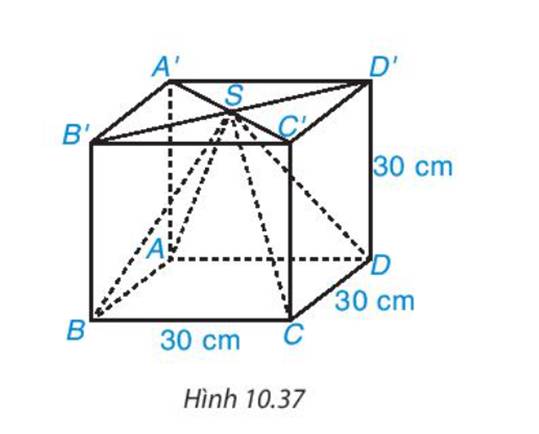
Diện tích mặt đáy của hình chóp tứ giác đều ABCD là: 30.30=900 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.900.30 = 9000(c{m^3})\)
- Thể tích hình lập phương là V=30.30.30=27000 (cm3)
Vậy thể tích phần gỗ bị cắt đi là V = 27000 − 9000=18000 (cm3)
Vẽ và cắt theo yêu cầu của đề bài.