Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 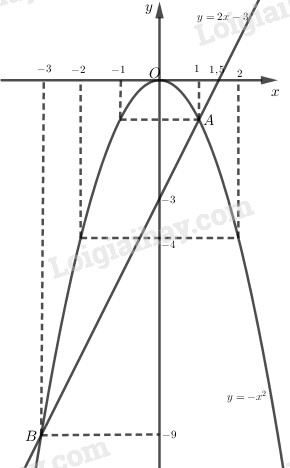
b: Phương trình hoành độ giao điểm là:
\(2x-3+x^2=0\)
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
Khi x=-3 thì y=-9
Khi x=1 thì y=-1
c: Khi x=1 và y=-1 thì \(2\cdot1-3=-1=y\)
Khi x=-3 và y=-9 thì \(2\cdot\left(-3\right)-3=-9=y\)
Khi x=1 và y=-1 thì \(-x^2=-1=y\left(nhận\right)\)
Khi x=-3 và y=-9 thì \(-x^2=-9=y\left(nhận\right)\)

a) Lập phương trình hoành độ giao điểm:
x2 = mx + 3
<=> x2 - mx - 3 = 0
Tọa độ (P) và (d) khi m = 2:
<=> x2 - 2x - 3 = 0
<=> \(\orbr{\begin{cases}x_1=3\\x_2=-1\end{cases}}\) => \(\orbr{\begin{cases}y_1=9\\y_2=1\end{cases}}\)
Tọa độ (P) và (d): A(3; 9) và B(-1; 1)
b) Để (P) và (d) cắt nhau tại 2 điểm phân biệt <=> \(\Delta>0\)
<=> (-m)2 - 4.1(-3) > 0
<=> m2 + 12 > 0 \(\forall m\)
Ta có: \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{3}{2}\)
<=> 2x2 + 2x1 = 3x1x2
<=> 2(x2 + x1) = 3x1x2
Theo viet, ta có: \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=m\\x_1x_2=\frac{c}{a}=-3\end{cases}}\)
<=> 2m = 3(-3)
<=> 2m = -9
<=> m = -9/2
Xét ptr hoành độ của `(P)` và `(D)` có:
`x^2/3=2x-3`
`<=>x^2=6x-9`
`<=>x^2-6x+9=0`
`<=>(x-3)^2=0`
`<=>x-3=0<=>x=3`
`=>y=2.3-3=3`
Vậy tọa độ giao điểm của `(P)` và `(D)` là: `(3;3)`