Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta cần chứng minh tam giác MNP là tam giác cân và có một góc bằng \(\frac{\Pi}{3}\)
Giả sử lục giacs có hướng âm, kí hiệu \(f\) là phép quay vec tơ theo góc \(-\frac{\Pi}{3}\) và M, N. P theo thứ tự là trung điểm FA, BC, DE
Khi đó AB=BO, CD=DO=OC, EF=FO=OE nên các tam giác ABO, CDO, EFO đều và có hướng âm
Suy ra \(f\left(\overrightarrow{AB}\right)=\overrightarrow{AO}\), \(f\left(\overrightarrow{OC}\right)=\overrightarrow{OD}\), \(f\left(\overrightarrow{FO}\right)=\overrightarrow{FE}\)
Từ đó ta có :
\(f\left(\overrightarrow{MN}\right)=f\left(\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{FC}\right)\right)=\frac{1}{2}\left(f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{FC}\right)\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AO}\right)+\overrightarrow{OD}+\overrightarrow{FE}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{FE}\right)\)
\(=\overrightarrow{MP}\)
Suy ra tam giác MNP cân và có góc PMN = \(\frac{\Pi}{3}\) => Điều phải chứng minh

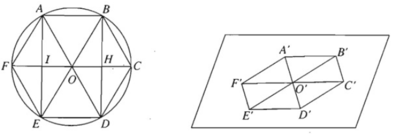
Với hình lục giác đều ABCDEF ta nhận thấy:
- Tứ giác OABC là hình bình hành ( vừa là hình thoi);
- Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O
Từ đó suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như sau: (h.2.54)
- Vẽ hình bình hành O'A'B'C' biểu diễn cho hình bình hành OABC..
- Lấy các điểm D', E', F' lần lượt đối xứng của A', B', C' qua tâm O', ta được hình biểu diễn A'B'C'D'E'F' của hình lục giác đều ABCDEF.
Chú ý. Ta có thể vẽ hình biểu diễn hình lục giác đều dựa trên sự phân tích sau đây ở hình thực ABCDEF (h.2.53) :
- Tứ giác ABDE là hình chữ nhật;
- Gọi I là trung điểm của cạnh AE và H là trung điểm của cạnh BD;
- Các điểm F và C đối xứng của O lần lượt qua I và H.
Từ đó ta có cách vẽ sau đây:
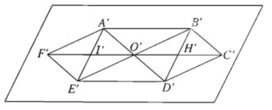
- Vẽ hình bình hành A'B'D'E' biểu diễn cho hình chữ nhật ABDE
- Gọi I' và H' lần lượt là trung điểm của A'E'và B'D'.
- Gọi F' đối xứng với O' qua I' và C' đối xứng với O' qua H', ta được hình biểu diễn A'B'C'D'E'F' của hình lục giác đều.

Đáp án C

Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O .
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4 n - 2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .
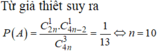

Đáp án A
Số các tam giác bất kỳ là n ( ω ) = C 18 3
Số các tam giác đều là 18 3 = 6
Có 18 các chọn một đỉnh của đa giác, mỗi đỉnh có 8 các chọn 2 đỉnh còn lại để được một tam giác đều
Số các tam giác cân là: 18.8 = 144
Số các tam giác cân không đều là: 144 - 6 = 138 => n(A) = 138
Xác suất => P(A) = 138 C 18 3 = 23 136

Đáp án A
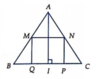
Gọi cạnh hình vuông là x. Ta có ![]()
![]()
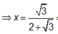
![]()
Gọi V 1 là thể tích hình nón khi quay tam giác ABC quanh trục trung tuyến AI , V 2 là thể tích hình trụ khi quay hình vuông MNPQ quanh trục AI thì
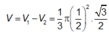
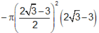
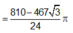




Tham khảo: