
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


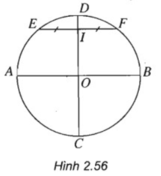
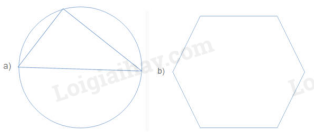
(h.2.56) Giả sử trên hình thực ta có đường tròn tâm O cùng với hai đường kính vuông góc của đường tròn đó là AB và CD. Nếu ta vẽ thêm một dây cung EF song song với AB thì đường kính CD sẽ đi qua trung điểm I của đoạn EF. Từ đó ta suy ra cách vẽ sau đây:
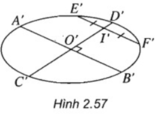
a) (h.2.57) Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính A'B' của hình elip đó. Đường kính này đi qua tâm O' của elip.
b) Vẽ một dây cung E'F' song song với đường kính A'B'. Gọi I' là trung điểm của E'F'. Đường thẳng O'I'cắt elip tại hai điểm C' và D'. Ta có A'B' và C'D' là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
Nhận xét. Hình bình hành A'C'B'D'là hình biểu diễn của hình vuông ACBD nội tiếp trong một đường tròn.

Đáp án A.
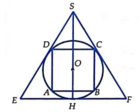
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ SEF đều” (hình vẽ).
![]()
=>Bán kính đáy và chiều cao của hình trụ (T) lần lượt là
![]()
và ![]()
Thể tích khối trụ là
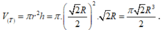
Ta có ∆ SEF đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của ∆ SEF.
Gọi H là trung điểm của EF thì
Hình vuông ABCD nội tiếp đường tròn (O) nên SH = 3OH = 3R![]()
Bán kính đáy và chiều cao của hình nón (N) lần lượt là ![]()
Thể tích khối nón là
![]()
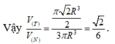

Với hình lục giác đều ABCDEF ta nhận thấy:
- Tứ giác OABC là hình bình hành ( vừa là hình thoi);
- Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O
Từ đó suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như sau: (h.2.54)
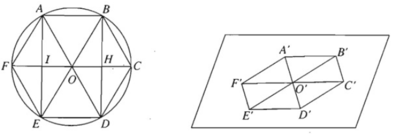
- Vẽ hình bình hành O'A'B'C' biểu diễn cho hình bình hành OABC..
- Lấy các điểm D', E', F' lần lượt đối xứng của A', B', C' qua tâm O', ta được hình biểu diễn A'B'C'D'E'F' của hình lục giác đều ABCDEF.
Chú ý. Ta có thể vẽ hình biểu diễn hình lục giác đều dựa trên sự phân tích sau đây ở hình thực ABCDEF (h.2.53) :
- Tứ giác ABDE là hình chữ nhật;
- Gọi I là trung điểm của cạnh AE và H là trung điểm của cạnh BD;
- Các điểm F và C đối xứng của O lần lượt qua I và H.
Từ đó ta có cách vẽ sau đây:
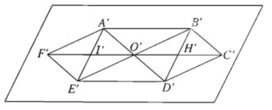
- Vẽ hình bình hành A'B'D'E' biểu diễn cho hình chữ nhật ABDE
- Gọi I' và H' lần lượt là trung điểm của A'E'và B'D'.
- Gọi F' đối xứng với O' qua I' và C' đối xứng với O' qua H', ta được hình biểu diễn A'B'C'D'E'F' của hình lục giác đều.


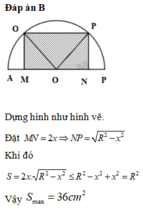
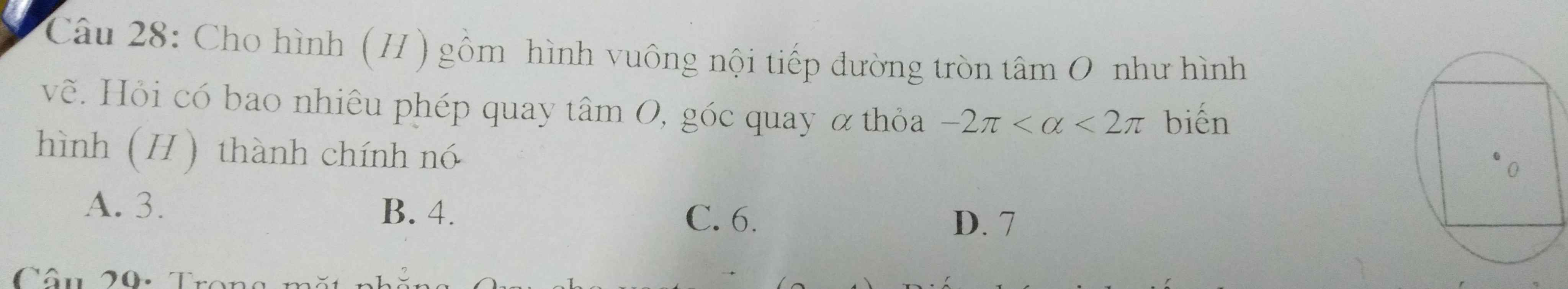

Tham khảo: