Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) góc xOy và góc yOz kề bù (GT)
=> góc xOy + góc yOz = 180 độ (t/c)
Mà góc xOy = 2 . góc yOz (GT)
=> 2 . góc yOz + góc yOz = 180 độ (t/c bắc cầu)
3 . góc yOz = 180 độ
góc yOz = 60 độ (1)
b) xOy và yOz là 2 góc kề bù (GT)
=> Ox và Oz đối nhau
xOy' và yOz là 2 góc đối đỉnh (do Oy và Oy' đối nhau; Ox và Oz đối nhau)
=> góc xOy' = góc yOz (2)
Từ (1) và (2) => góc xOy' = 60 độ (t/c bắc cầu)
c) Các cặp góc đối đỉnh: xOy' và yOz; xOy và y'Oz

Ta có xOy + yOz = 180o (kề bù)
Mà xOy = 2yOz <=> \(\frac{xOy}{2}=\frac{yOz}{1}=\frac{xOy+yOz}{2+1}=\frac{180^o}{3}=60^o\)
=> xOy = 60o . 2 = 120o
yOz = 60o . 1 = 60o

Lời giải:
a. Hai góc kề bù:
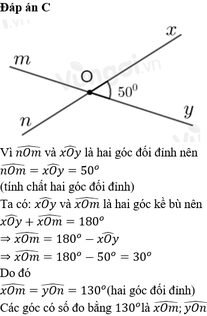
$\widehat{xOy}$ và $\widehat{yOm}$
b.
Vì $\widehat{xOy}$ và $\widehat{yOm}$ kề bù nên:
$\widehat{xOy}+\widehat{yOm}=180^0$
$\widehat{yOm}=180^0-\widehat{xOy}=180^0-60^0=120^0$
c.
Vì $Om$ là phân giác $\widehat{xOy}$ nên $\widehat{yOt}=\widehat{xOt}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}.60^0=30^0$
$\widehat{xOt}$ và $\widehat{tOm}$ là 2 góc kề bù nên:
$\widehat{xOt}+\widehat{tOm}=180^0$
$\widehat{tOm}=180^0-\widehat{xOt}=180^0-30^0=150^0$

Ta có hình vẽ:
x O z y y'
a) Ta có: xOy + yOz = 180o (kề bù)
=> 2.yOz + yOz = 180o
=> 3.yOz = 180o
=> yOz = 180o : 3 = 60o
b) Có: xOy = 2.yOz = 2.60o = 120o
c) Vì xOy và yOz là 2 góc kề bù nên Ox và Oz là 2 tia đối nhau
Mà Oy' và Oy là 2 tia đối nhau
Như vậy, các cặp góc đối đỉnh là: xOy và zOy'; zOy và xOy'


a) Hai góc kề bù có trên hình vừa vẽ là góc xOy và mOy
b) Vì \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {yOm} = 180^\circ \\ \Rightarrow \widehat {yOm} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
c) Vì tia Ot là tia phân giác của góc xOy nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOt} + \widehat {tOm} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {tOm} = 180^\circ \\ \Rightarrow \widehat {tOm} = 180^\circ - 30^\circ = 150^\circ \end{array}\)
Vậy \(\widehat {tOy} = 30^\circ ;\widehat {tOm} = 150^\circ \)
a, \(\widehat{xOy}\) + \(\widehat{yOz}\) = 1800; \(\widehat{xOy}\) = \(\widehat{yOz}\) ⇒ 2\(\widehat{xOy}\) = 1800
⇒ \(\widehat{yOz}\) = \(\widehat{xOy}\) = 1800 : 2 = 900
b, Các cặp góc bằng nhau là:
\(\widehat{yOz}\) = \(\widehat{xOm}\); \(\widehat{yOz}\) = \(\widehat{xOy}\); \(\widehat{yOz}\) = \(\widehat{zOm}\);
\(\widehat{zOm}\) = \(\widehat{mOx}\); \(\widehat{zOm}\) = \(\widehat{xOz}\);
\(\widehat{xOm}\) = \(\widehat{xOy}\);