K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PH
2
28 tháng 10 2015
x | 0 | 1 | |
| x | - | 0 + | + |
| 1-x | - | - | 0 + |
| y | -1 | 2x-1 | 1 |
xét khoảng với:+) X<0 => y=-1
+) 0=<x<=1 => y =2x-1
+) x>1 => y =1...
vẽ hàm số bình thường...sau đó chỉ lấy x thỏa mãn trên khoảng txđ
NT
4
16 tháng 11 2015
a)Ta có bảng sau
| x | -1 | 0 | |||
| x+1 | - | 0 | + | / | + |
| x | - | / | - | 0 | + |
(+) với x < -1 ta có y = -x + -x - 1 = -2x - 1
(+) với -1 <= x <= 0 ta có y = -x + x + 1 = 1
(+) với x >0 ta có y = x + x + 1 = 2x + 1
11 tháng 4 2023
b: PTHĐGĐ là:
1/2x^2-x-4=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
=>y=8 hoặc y=2
a: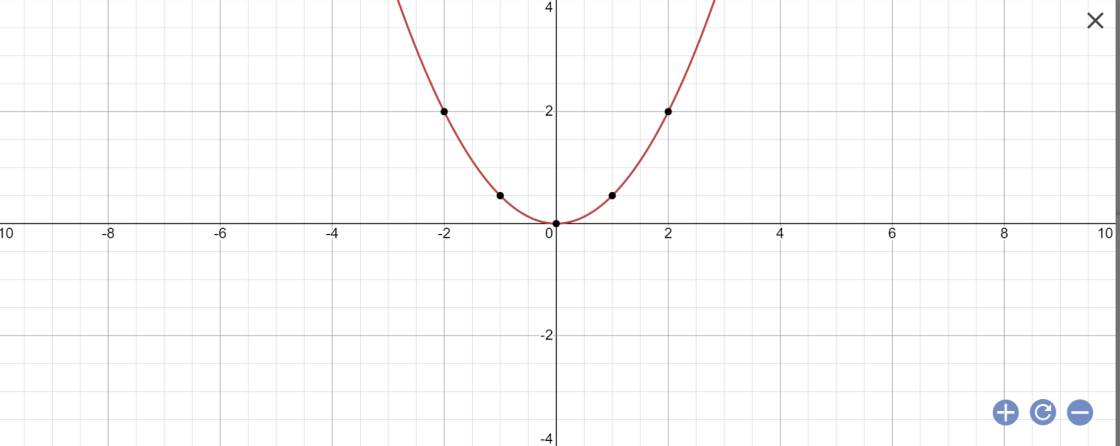 
ST
1
28 tháng 5 2015
a) y = x2 : Vẽ parabol đi qua 3 điểm O(0;0); (1;1) ; (-1;1)
y = 3x - 1: Tìm 2 điểm thuộc đồ thị: Chọn điểm A(0;-1), B (1;2). Đồ thị hàm số y = 3x - 1 là đường thẳng đi qua 2 điểm A; B
b) Hoành độ giao điểm là nghiệm của phương trình:
x2 = 3x - 1 <=> x2 - 3x - 1 = 0
\(\Delta\) = (-3)2 - 4.1.(-1) = 13
=> x1 = \(\frac{3+\sqrt{13}}{2}\) ; x2 = \(\frac{3-\sqrt{13}}{2}\)
Gọi 2 giao điểm là M(x1; y1); N (x2; y2)
y1 = 3x1 - 1 = \(\frac{9+9\sqrt{13}}{2}\) - 1 = \(\frac{7+3\sqrt{13}}{2}\)
y2 = 3x2 - 1 = \(\frac{9-3\sqrt{13}}{2}\) - 1 = \(\frac{7-3\sqrt{13}}{2}\)
Vậy........
2 tháng 2 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x^2-x-4=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-8=0\\y=x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-4\right)\left(x+2\right)=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(4;8\right);\left(-2;2\right)\right\}\)