
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C 3cm 4cm
độ dài cạnh huyền BC là 5 cm
bình phương độ dài cạnh huyền BC là 5^2 =25
tổng bình phương 2 cạnh góc vuông làác vuông bình phương cạnh huyền = bình phương tổng 2 cạnh góc vuông

IK2=HI2 +HK2=32+42 =25 (định lý pitago) ⇒IK=5cm

trả lời
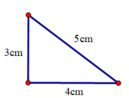
Hai cạnh góc vuông của một tam giác vuông có độ dài lần lượt bằng 3cm và 4cm.
Độ dài cạnh huyền của tam giác đó bằng.....5 cm....... cm.
hc tốt

Theo bài ra ta có: Độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Nên ta có:
\(\frac{AB}{3}=\frac{AC}{4}\) \(\Rightarrow\left(\frac{AB}{3}\right)^2=\left(\frac{AC}{4}\right)^2\) \(\Rightarrow\frac{AB^2}{9}=\frac{AC^2}{16}\)
Theo định lí Py-ta-go, tam giác vuông ABC có cạnh huyền BC \(\Rightarrow AB^2+AC^2=BC^2=4^2=16\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{9+16}=\frac{16}{25}\)
\(\Rightarrow\frac{AB^2}{9}=\frac{16}{25}\Rightarrow AB^2=5,76\Rightarrow AB=2,4\left(cm\right)\)
\(\frac{AC^2}{16}=\frac{16}{25}\Rightarrow AC^2=10,24\Rightarrow AC=3,2\left(cm\right)\)
Vậy AB = 2,4 cm
AC = 3,2 cm
BC = 4 cm

a) Do \(MF>ME\) nên \(\widehat{E}>\widehat{F}\) (Quan hệ giữa góc và cạnh đối diện trong tam giác)
b) Áp dụng định lý Pytago ta có:
\(EF^2=ME^2+MF^2=3^2+4^2=25\Rightarrow EF=5\left(cm\right)\)
Do \(MI\) là trung tuyến ứng với cạnh huyền nên \(MI=\dfrac{1}{2}EF=2,5\left(cm\right)\)
Do \(G\) là trọng tâm tam giác nên \(MG=\dfrac{2}{3}MI=\dfrac{2}{3}.2,5=\dfrac{5}{3}\left(cm\right)\)

Gọi độ dài cạnh huyền là x cm
Áp dụng định lý Pitago ta có 32+42=x2
=> x2=9+16=25
=>x=5
Ta có: ch2 = 32 + 42 = 9 + 16 = 25 => ch = 5 cm