Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc tọa độ tại H.
Pt chuyển động của H và h lần lượt là:
\(x_H=v_0t+\dfrac{1}{2}at^2\)
\(x_h=\left(H-h\right)+\dfrac{1}{2}at^2\)
Mà hai vật rơi xuống cùng lúc:
\(\Rightarrow x_H=x_h\)\(\Rightarrow v_0t=H-h\Rightarrow t=\dfrac{H-h}{v_0}\)
\(h=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot g\cdot\left(\dfrac{H-h}{v_0}\right)^2\)
\(\Rightarrow v_0=\left(H-h\right).\sqrt{\dfrac{\dfrac{1}{2}g}{h}}\)(m/s)
gốc tọa độ tại H
yH= v0.t+g.t2.0,5
yh=(H-h)+g.t2.0,5
hai vật rơi xuống cùng lúc tức t như nhau
yH=yh⇒t=H−h/v0⇒t=H−h/v0
⇒h=g.0,5,(H−h/v0)^2⇒v0=(H-h).√g.0,5/h.
mik viết hơi rối thông cảm <3

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

a) thời gian rơi của vật
t=\(\sqrt{\dfrac{s}{0,5.g}}\)=2s
b)vận tốc khi chạm đất
v=g.t=20m/s
c) vận tốc trước khi chạm đất 1s hay vận tốc khi vật rơi được 1s
v=g.t=10m/s2
d) quãng đường vật rơi được với t-1 giây là
s1=g.0,5.(t-1)2=5m
quãng đường rơi được trong giây cuối cùng
\(\Delta\)s=s-s1=15m

Đáp án D
Chọn gốc tọa độ O tại mặt đất, chiều (+) hướng thẳng đứng lên trên, gốc thời gian lúc I rơi
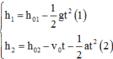
Hai vật rơi đến đất cùng lúc nên ta có:
![]()
Từ (1):
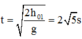
![]()
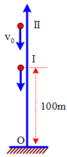

vận dụng công thức sau để giải:
∆x = (v0+v).∆t / 2
∆t là thời gian vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.
Lưu ý ở bài này giây thứ 1 tính từ thời điểm t=0 đến t=1
Giây thứ 4 tính từ thời điểm t=3 đến t=4
(**) Công thức không phụ thuộc thời gian trong chuyển động thẳng biến đổi đều :
v^2 - v0^2 = 2.a.∆x
Với a là gia tốc, vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.

gốc tọa độ tại H
yH= v0.t+g.t2.0,5
yh=(H-h)+g.t2.0,5
hai vật rơi xuống cùng lúc tức t như nhau
yH=yh\(\Rightarrow t=\dfrac{H-h}{v_0}\)
\(\Rightarrow\)h=\(g.0,5,\left(\dfrac{H-h}{v_0}\right)^2\)\(\Rightarrow\)v0=\(\left(H-h\right).\sqrt{\dfrac{g.0,5}{h}}\)