Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Sử dung̣ đường tròn lương̣ giác
Cách giải:
Theo bài ra ta có:
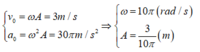
Thời điểm ban đầu vật ở vị trí (1) có v = v0/2
Khi
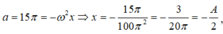
vật ở vị trí (2)
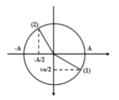
Từ hình vẽ xác định được thời điểm vật ở vị trí (2) là 5T/12 = 0,083s

Đáp án C
Giả sử phương trình dao động của vật có dạng : x = A cos ( ω t + φ )
ω = a m a x v m a x = 10 π rad / s
Biên độ : A = v m a x ω = 3 10 π m
Vận tốc của vật : v = x' = - ω A si n ( 10 πt + φ ) = - 3 sin ( 10 πt + φ ) m / s
v 0 = - 3 sin φ = 1,5 m/s ⇒ sin φ = - 0 , 5 s và do thế năng đang tăng nên chọn φ = - π 6

Phương trình có hai họ nghiệm 10 πt - π 6 = ± 2 π 3 ± 2 kπ
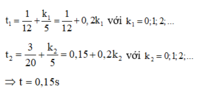

Đáp án C
+ t = 0 : v = + v m ax 2 ⇒ x = A 3 2 . Lúc này thế năng đang tăng suy ra x = A 3 2 và vật đi theo chiều dương.
+ thời điểm t : a = a m ax 2 ⇒ x = − A 2
Vòng tròn đơn vị :
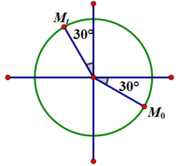
Vị trí của vật ở thời điểm t = 0 (M0) và t (Mt) như trên hình vẽ. Dễ dàng tìm được góc quét bằng 150 ° , tương ứng với Δ t = 5 T 12 .
Có
ω
=
a
m
ax
v
m
ax
=
10
π
⇒
T
=
0
,
2
(
s
)
⇒
Δ
t
=
0
,
083
(
s
)

\(v_{max}=\omega A=16\left(cm/s\right);a_{max}=\omega^2A=128\left(cm/s^2\right)\)
\(\Rightarrow\dfrac{a_{max}}{v_{max}}=\omega=8\left(rad/s\right)\Rightarrow A=\dfrac{16}{8}=2\left(cm\right)\)
\(x=1\Rightarrow\varphi=arc\cos\left(\dfrac{1}{2}\right)=\dfrac{\pi}{3}\)
\(\Rightarrow x=2\cos\left(8t+\dfrac{\pi}{3}\right)\left(cm\right)\)
Đề nghị bạn ko đăng những câu trả lời ko rõ ràng chi tiết và quan trọng là nó ko liên quan đến câu đang được hỏi. Kiếm GP kiểu này ko hay đâu. Mình xin phép xóa bài nhé !
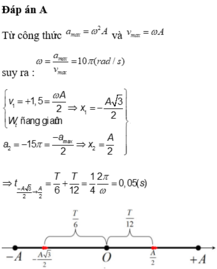

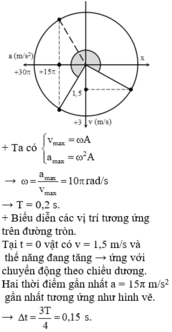
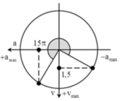

\(\omega=\dfrac{a_{max}}{v_{max}}=10\pi\) =>T=0,2(s)
Lúc t=0, v=-1,5m/s=\(-\dfrac{v_{max}}{2}\)=>x=\(\pm\dfrac{A\sqrt{3}}{2}\) kết hợp dữ kiện vận tốc âm và thế năng đang giảm =>x=\(\dfrac{A\sqrt{3}}{2}\)va đang hướng về VTCB
Khi gia tốc a=-15π=\(-\dfrac{a_{max}}{2}\)=>x=\(\dfrac{A}{2}\)
=>△t=\(\dfrac{T}{6}-\dfrac{T}{12}=\)0,01(6) s