Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Ta có: v m a x = ω A a m a x = ω 2 A → ω = a m a x v m a x → T = 2 π v m a x a m a x = 2 π 1 1 , 57 = 4

\(\omega=\dfrac{a_{max}}{v_{max}}=10\pi\) =>T=0,2(s)
Lúc t=0, v=-1,5m/s=\(-\dfrac{v_{max}}{2}\)=>x=\(\pm\dfrac{A\sqrt{3}}{2}\) kết hợp dữ kiện vận tốc âm và thế năng đang giảm =>x=\(\dfrac{A\sqrt{3}}{2}\)va đang hướng về VTCB
Khi gia tốc a=-15π=\(-\dfrac{a_{max}}{2}\)=>x=\(\dfrac{A}{2}\)
=>△t=\(\dfrac{T}{6}-\dfrac{T}{12}=\)0,01(6) s

+ Từ phương trình v = 10 π c os 2 π t + 0 , 5 π = ω A cos 2 π t + φ + π 2
® x = 5 cos 2 π t .
® Quỹ đạo dao động là: L = 2 A = 10 cm
Tốc độ cực đại là v max = 10 π cm/s
Gia tốc cực đại là a max = ω 2 A = 20 π 2 c m / s 2
Tốc độ trung bình trong một chu kì là v t b = s T = 4 A T = 4.5 1 = 20 cm/s.
Tại t = 0 thì x = 5 ® vật ở vị trí biên.
® Các phát biểu đúng là: c, e.
Đáp án C

Đáp án C
Phương pháp: Áp dụng công thức tính tốc độ cực đại của vật dao động điều hòa
Cách giải:
Ta có vmax = ωA =>ω = vmax/A = 2π rad/s
=> Chu kì dao động: T = 2π/ω = 1 s => Chọn C

Đáp án C
Giả sử phương trình dao động của vật có dạng : x = A cos ( ω t + φ )
ω = a m a x v m a x = 10 π rad / s
Biên độ : A = v m a x ω = 3 10 π m
Vận tốc của vật : v = x' = - ω A si n ( 10 πt + φ ) = - 3 sin ( 10 πt + φ ) m / s
v 0 = - 3 sin φ = 1,5 m/s ⇒ sin φ = - 0 , 5 s và do thế năng đang tăng nên chọn φ = - π 6

Phương trình có hai họ nghiệm 10 πt - π 6 = ± 2 π 3 ± 2 kπ
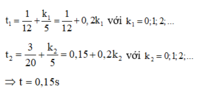
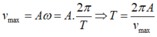

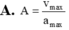
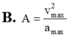
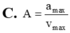
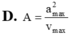
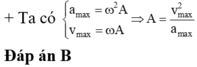
a0=w.v0 \(\Rightarrow\)w=6 rad/s=\(\dfrac{2\pi}{T}\) Suy ra T=
x2+ \(\dfrac{v^2}{w^2}\)=A2
Suy ra A