Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 : \(\frac{2}{3}< \left[\frac{1}{6}+\frac{2}{15}+\frac{3}{40}+\frac{4}{96}\right]:5\times x< \frac{5}{6}\)
=> \(\frac{2}{3}< \left[\frac{1}{6}+\frac{2}{15}+\frac{3}{40}+\frac{1}{24}\right]:5\cdot x< \frac{5}{6}\)
=> \(\frac{2}{3}< \left[\frac{1}{6}+\frac{1}{24}+\frac{2}{15}+\frac{3}{40}\right]:5\cdot x< \frac{5}{6}\)
=> \(\frac{2}{3}< \frac{5}{12}:5\cdot x< \frac{5}{6}\)
=> \(\frac{2}{3}< \frac{1}{12}\cdot x< \frac{5}{6}\)
=> \(\frac{2}{3}< \frac{x}{12}< \frac{5}{6}\)
=> \(\frac{8}{12}< \frac{x}{12}< \frac{10}{12}\)
=> x = 9
Bài 2 : \(\frac{\left[\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right]}{x}=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{132}\)
=> \(\frac{\left[1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}\right]}{x}=\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{11\cdot12}\)
=> \(\frac{\left[1-\frac{1}{16}\right]}{x}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{11}-\frac{1}{12}\)
=> \(\frac{15}{\frac{16}{x}}=1-\frac{1}{12}\)
=> \(\frac{15}{\frac{16}{x}}=\frac{11}{12}\)
=> \(\frac{15}{16}:x=\frac{11}{12}\)
=> \(x=\frac{45}{44}\)
Bài 3 : \(\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{1}{x\times(x+1):2}=\frac{399}{400}\)
=> \(\frac{2}{6}+\frac{2}{12}+\frac{2}{20}+...+\frac{2}{x\times(x+1)}=\frac{399}{400}\)
=> \(2\left[\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{x\times(x+1)}\right]=\frac{399}{400}\)
=> \(2\left[\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{x\times(x+1)}\right]=\frac{399}{400}\)
=> \(\left[\frac{1}{2}-\frac{1}{3}+...+\frac{1}{x}-\frac{1}{x+1}\right]=\frac{399}{800}\)
=> \(\frac{1}{2}-\frac{1}{x+1}=\frac{399}{800}\)
=> \(\frac{1}{x+1}=\frac{1}{800}\)
=> x = 799
Bài 2 :
\(\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right):x=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{132}\) (*)
Ta có : \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{8}{16}+\frac{4}{16}+\frac{2}{16}+\frac{1}{16}=\frac{8+4+2+1}{16}=\frac{15}{16}\) (1)
Lại có : \(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{132}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{11.12}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{11}-\frac{1}{12}\)
\(=1\left(-\frac{1}{2}+\frac{1}{2}\right)+\left(-\frac{1}{3}+\frac{1}{3}\right)+...+\left(-\frac{1}{11}+\frac{1}{11}\right)-\frac{1}{12}\)
\(=1-\frac{1}{12}=\frac{11}{12}\) (2)
Thay (1) và (2) vào biểu thức (*) ta được :
\(\frac{15}{16}:x=\frac{11}{12}\)
\(\Leftrightarrow x=\frac{15}{16}:\frac{11}{12}\)
\(\Leftrightarrow x=\frac{45}{44}\)
Vậy : \(x=\frac{45}{44}\)

Xếp theo thứ tự là :
\(\frac{2}{7};\frac{1}{3};\frac{3}{5};\frac{7}{8};\frac{4}{3}\)
học tốt
xin tiick
3/5,2/7, 1/3, 4/3, 7/8
THỨ TỰ TỪ BÉ ĐẾN LỚN :
=> 2/7 ; 1/3 ; 3/5 ; 7/8 ; 4/3

a, \(1\frac{2}{7}+6\frac{5}{6}=\frac{9}{7}+\frac{41}{6}=\frac{54}{42}+\frac{287}{42}=\frac{341}{42}\)

a) x + 2/3=9/11
<=> x=9/11-2/3= 5/33
b) x - 3/10=4/15
<=> x=4/15+3/10=17/30
c) X x 1/7=5/6
<=> x=5/6:1/7=35/6
d) x : 3/5=1/6
<=> x=1/6x3/5=1/10
\(a,x+\frac{2}{3}=\frac{9}{11}\)
\(x=\frac{9}{11}-\frac{2}{3}\)
\(x=\frac{5}{33}\)
\(b,x-\frac{3}{10}=\frac{4}{15}\)
\(x=\frac{4}{15}+\frac{3}{10}\)
\(x=\frac{17}{30}\)
\(c,x\cdot\frac{1}{7}=\frac{5}{6}\)
\(x=\frac{5}{6}:\frac{1}{7}\)
\(x=\frac{35}{6}\)
\(d,x:\frac{3}{5}=\frac{1}{6}\)
\(x=\frac{1}{6}\cdot\frac{3}{5}\)
\(x=\frac{1}{10}\)
. là nhân nha


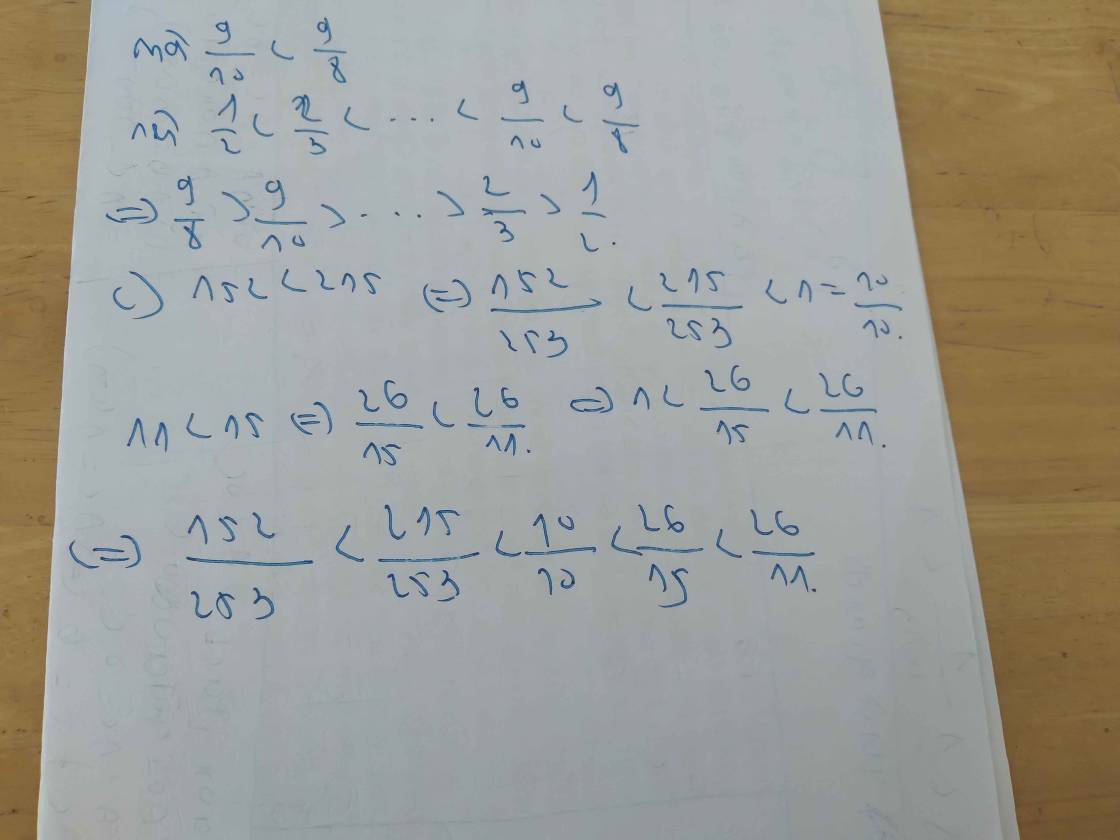
Nhắc lại:- Tử bé hơn mẫu thì phân số bé hơn 1, tử lớn hơn mẫu thì phân số lớn hơn 1, tử bằng mẫu thì bằng 1;
- Trong 2 phân số cùng mẫu, tử của phân số nào lớn hơn thì phân số đó lớn hơn;
- Trong 2 phân số cùng tử, mẫu của phân số nào lớn hơn thì phân số đó bé hơn;
- Bất đẳng thức \(\frac{a}{b}< \frac{a+c}{b+c}\) với \(\frac{a}{b}< 1\) \(a;b;c\ne0;\infty\)
a) Ta có \(\frac{26}{15}>1;\frac{215}{253}< 1;\frac{10}{10}=1;\frac{26}{11}>1;\frac{152}{253}< 1\).
Mà \(\frac{152}{253}< \frac{215}{253};\frac{26}{11}>\frac{26}{15}\) nên đáp án là \(\frac{152}{253};\frac{215}{253};\frac{10}{10};\frac{26}{15};\frac{26}{11}\)
b) Dựa vào bất đẳng thức \(\frac{a}{b}< \frac{a+c}{b+c}\) với \(a;b;c\ne0;\infty\) ta có đáp án là \(\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};\frac{5}{6}\)
a) 152/253 ; 215/253 ; 10/10 ; 26/15 ; 26/11
b) 1/2 ; 4/5 ; 2/3 ; 3/4 ; 5/6